With the development of power electronics technology, various non-linear loads have been widely used in industrial and agricultural production and transmission equipment, making the distortion of the power grid waveform, that is, the harmonic interference more and more serious. Waveform distortion of the power grid will bring many harms, such as increasing the loss of motors, transformers, reactors, etc., interfering with communication lines, and causing partial or even paralysis of the entire power grid. In order to better suppress the harmonics, it is necessary to accurately analyze the harmonic interference of the power grid. In the process of sampling and discretizing periodic signals, two methods are usually used. One is quasi-synchronous sampling, which requires more waveforms and uses quasi-synchronous algorithms to perform a large number of iterative operations, which is not suitable for the measurement of dynamic signals; the other is One is synchronous sampling, which is divided into hardware synchronous sampling and software synchronous sampling. Hardware synchronous sampling adopts a phase-locked loop circuit, which is generally complicated in design and low reliability; software synchronous sampling does not require additional hardware circuits, and its implementation method is flexible. It has been widely used in the measurement of periodic signals. Because the AC signal is a special periodic signal, its spectrum is a line spectrum distributed on the fundamental wave and its integer multiples of frequency. It is necessary to ensure that the sampling signal and the original signal are strictly synchronized, that is, the sampling frequency is an integer multiple of the signal frequency, otherwise it will The occurrence of spectrum leakage makes the result of discrete Fourier transform of the signal produce test errors and affects the accuracy of harmonic analysis. Due to the small fluctuations in the frequency of the power grid, it is inevitable that the above phenomenon occurs when the sampling rate is fixed. For this reason, domestic and foreign scholars have proposed many methods to reduce the influence of spectrum leakage on measurement accuracy.
Spectrum Leakage
The so-called spectrum leakage refers to the mutual influence between the various spectral lines in the signal spectrum, causing the measurement result to deviate from the actual value, and at the same time appear on other frequency points on both sides of the spectral line Some false spectra with smaller amplitudes. Simply put, the cause of spectrum leakage is that the sampling frequency is not synchronized with the signal frequency, causing the phase of the periodic sampling signal to be discontinuous at the beginning and the end.
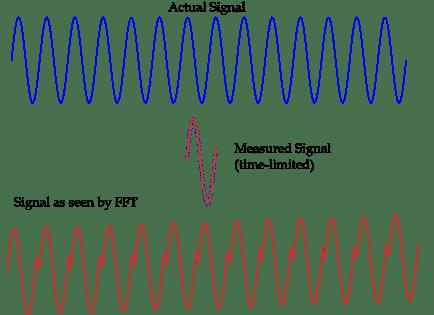
The so-called spectrum leakage is the mutual influence between the various spectral lines in the signal spectrum, which makes the measurement result deviate from the actual value. False spectrum. Using FFT to analyze the harmonics in the power system, it is impossible to avoid the problem of spectrum leakage. This is mainly due to the inherent nonlinearity, randomness, distribution, non-stationarity and complexity of influencing factors. The frequency is not always a constant value of the rated power frequency, it will change within a range around the rated power frequency, so that it cannot be guaranteed that the real-time frequency is an integer multiple of the fundamental frequency, and synchronous sampling cannot be achieved. .
Methods for suppressing spectrum leakage proposed at home and abroad
The most direct impact of spectrum leakage is the inaccuracy of harmonic analysis, which in turn leads to inaccurate electrical parameter measurement based on harmonic analysis. precise. Increasing the number of data sampling points can reduce leakage, the essence of which is to reduce the width of the main lobe of the rectangular window. Increasing the sampling frequency of the signal can also reduce leakage. Compared with the increased amount of data processing, the above two methods have extremely limited improvement in leakage. The literature proposes window functions and interpolation techniques. The basic principle of selecting window function is to require narrow main lobe and small side lobe, so that these two requirements can be taken into account as much as possible, and Hanning window is usually selected. From the time domain, adding the Hanning window actually makes the phase of the starting point and ending point of the periodic sampling signal 0, which overcomes the phenomenon that the phase of the sampling signal is discontinuous at the beginning and the end due to frequency fluctuations, but any window function is Can not solve the error caused by the deviation of the zero point at the main lobe, so the reduction of leakage is also limited. Interpolation technology can almost completely eliminate the influence of leakage, but the data processing volume of this algorithm is too large, and the real-time performance is difficult to guarantee. The literature proposes an algorithm to reduce spectrum leakage. Its core is that when the product of the sampling period and the number of sampling points is equal to an integer multiple of the signal period, the discrete sequence obtained by the algorithm is the sampling sequence of the signal. Otherwise, the algorithm will automatically adjust the sampling. sequence. The simulation proves that the algorithm improves the spectrum leakage more obviously when the signal frequency fluctuation is not large, and the accuracy of the algorithm is lower when the signal frequency fluctuation is large. The general feature of the above algorithm is to correct the sampling sequence or frequency spectrum, without solving the root cause of the spectrum leakage. This determines that the above algorithm or effect is not significant, or the real-time performance is poor. The root cause of spectrum leakage is fs≠Nf0. Only by adjusting fs in real time to make fs=Nf0 can the spectrum leakage be effectively solved. Based on the above purpose, an algorithm for adaptively adjusting the sampling rate is proposed, and the simulation proves the effectiveness of the algorithm.
The main factor that affects the speed of this algorithm is FFT. In recent years, with the emergence of DSP chips that are particularly suitable for data processing and their applications in periodic signal analysis, FFT operations have become faster and faster.Using VC5402 to perform 1024-point complex FFT operations only takes 40 μs, which is completely satisfactory. System real-time requirements. Therefore, this algorithm has strong practical value in the system based on AC signal measurement. The algorithm is currently being applied to the design of the monitoring system of hydropower stations.
Spectrum leakage in Fourier transform profilometry
Fourier transform profilometry (FTP) is a commonly used three-dimensional surface measurement method. Its working principle consists of the following three parts: 1) The surface shape of the three-dimensional object under test spatially modulates the structured light field of the grating, so that the deformed structured light field carries the information of the height distribution of the three-dimensional surface shape; 2) For continuous distribution The deformed structured light field is sampled to obtain discrete information for easy computer processing; 3) The computer performs Fourier transform on the obtained discrete information, selects an appropriate filter window to filter out the fundamental frequency component from the spectrum, and reverses the fundamental frequency component. The Fourier transform restores the height distribution of the measured surface.
When Fourier transform is performed on the discrete deformed structured light field, the discrete Fourier transform algorithm requires the periodic expansion of the deformed structured light field in the space domain. The period extension may cause spectrum leakage, so errors will be introduced in the Fourier transform profilometry measurement, but few people discuss it theoretically. In order to reduce the spectrum leakage caused by period expansion, people often choose an appropriate window function (such as Hanning window) to weight the deformed light field, so that the deformed light field sampled by the CCD is processed by the window function and the edge intensity of the window is 0, and then Fourier transform. However, after the signal is processed by the window function, some information will be lost, which is equivalent to reducing the spectrum leakage while also introducing errors. This paper analyzes the problem of spectrum leakage of deformed light field with limited space. The relationship between the extended period and the optical field spectrum leakage of the deformed structure is theoretically deduced, and the calculation method and quantitative analysis of the error are given. It is pointed out that only when the expansion period is equal to an integer multiple of the grating period, the expanded fringes are continuous, and the Fourier transform does not cause spectrum leakage; when the expansion period is not equal to an integer multiple of the grating period, the expanded fringes are discontinuous. Especially when there is a difference of 0.5 grating period between the expansion period and the integer multiple of the deformed light field grating period, the fringe breakage is the most serious after the expansion, and the spectrum leakage is the largest. Therefore, when measuring with Fourier transform profilometry, try to choose the expansion period equal to an integer multiple of the signal period to reduce the measurement error caused by spectrum leakage. If this is not possible, an iterative method can be used to extrapolate fringes to generate new fringes on both sides of the effective field of view to extend the leakage error beyond the effective field of view and reduce the edge leakage error.
