Con lo sviluppo della tecnologia dell'elettronica di potenza, vari carichi non lineari sono stati ampiamente utilizzati nelle apparecchiature di produzione e trasmissione industriale e agricola, rendendo sempre più grave la distorsione della forma d'onda della rete elettrica, ovvero l'interferenza armonica. La distorsione della forma d'onda della rete elettrica porterà molti danni, come l'aumento della perdita di motori, trasformatori, reattori, ecc., interferendo con le linee di comunicazione e causando la paralisi parziale o addirittura dell'intera rete elettrica. Per meglio sopprimere le armoniche, è necessario analizzare accuratamente l'interferenza armonica della rete elettrica. Nel processo di campionamento e discretizzazione dei segnali periodici, vengono solitamente utilizzati due metodi. Uno è il campionamento quasi sincrono, che richiede più forme d'onda e utilizza algoritmi quasi sincroni per eseguire un gran numero di operazioni iterative, che non è adatto alla misurazione di segnali dinamici; l'altro è Uno è il campionamento sincrono, che è diviso in campionamento sincrono hardware e campionamento sincrono software. Il campionamento sincrono hardware adotta un circuito ad anello ad aggancio di fase, che è generalmente complicato nella progettazione e bassa affidabilità; il campionamento sincrono software non richiede circuiti hardware aggiuntivi e il suo metodo di implementazione è flessibile. È stato ampiamente utilizzato nella misurazione di segnali periodici. Poiché il segnale AC è un segnale periodico speciale, il suo spettro è uno spettro lineare distribuito sull'onda fondamentale e sui suoi multipli interi di frequenza. È necessario garantire che il segnale di campionamento e il segnale originale siano strettamente sincronizzati, ovvero che la frequenza di campionamento sia un multiplo intero della frequenza del segnale, altrimenti lo sarà Il verificarsi di dispersione dello spettro rende il risultato della trasformata discreta di Fourier del segnale producono errori di test e influenzano l'accuratezza dell'analisi armonica. A causa delle piccole fluttuazioni nella frequenza della rete elettrica, è inevitabile che il fenomeno di cui sopra si verifichi quando la frequenza di campionamento è fissa. Per questo motivo, studiosi nazionali e stranieri hanno proposto molti metodi per ridurre l'influenza della perdita di spettro sull'accuratezza della misurazione.
Perdita di spettro
La cosiddetta perdita di spettro si riferisce all'influenza reciproca tra le varie linee spettrali nello spettro del segnale, facendo sì che il risultato della misurazione si discosti dal valore effettivo e allo stesso tempo appaia su altri punti di frequenza su entrambi i lati della linea spettrale Alcuni falsi spettri con ampiezze minori. In poche parole, la causa della dispersione dello spettro è che la frequenza di campionamento non è sincronizzata con la frequenza del segnale, causando una discontinuità della fase del segnale di campionamento periodico all'inizio e alla fine.
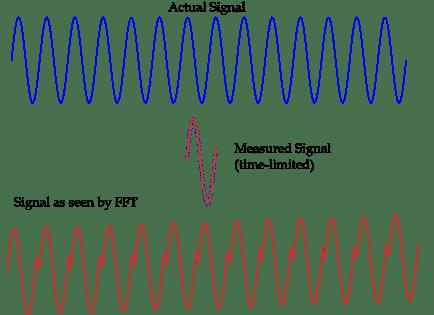
La cosiddetta perdita di spettro è l'influenza reciproca tra le varie linee spettrali nello spettro del segnale, che fa deviare il risultato della misurazione dal valore effettivo. Falso spettro. Utilizzando FFT per analizzare le armoniche nel sistema di alimentazione, è impossibile evitare il problema della dispersione dello spettro. Ciò è dovuto principalmente alla non linearità intrinseca, alla casualità, alla distribuzione, alla non stazionarietà e alla complessità dei fattori di influenza. La frequenza non è sempre un valore costante della frequenza di alimentazione nominale, cambierà entro un intervallo intorno alla frequenza di alimentazione nominale, quindi non è possibile garantire che la frequenza in tempo reale sia un multiplo intero della frequenza fondamentale e il campionamento sincrono non può essere raggiunto. .
Metodi per sopprimere la perdita di spettro proposti in patria e all'estero
L'impatto più diretto della perdita di spettro è l'imprecisione dell'analisi armonica, che a sua volta porta a una misurazione imprecisa dei parametri elettrici basata sull'analisi armonica. preciso. L'aumento del numero di punti di campionamento dei dati può ridurre le perdite, la cui essenza è ridurre la larghezza del lobo principale della finestra rettangolare. Anche l'aumento della frequenza di campionamento del segnale può ridurre le perdite. Rispetto alla maggiore quantità di elaborazione dei dati, i due metodi di cui sopra hanno un miglioramento estremamente limitato della perdita. La letteratura propone funzioni finestra e tecniche di interpolazione. Il principio di base della selezione della funzione della finestra è di richiedere un lobo principale stretto e un lobo laterale piccolo, in modo che questi due requisiti possano essere presi in considerazione il più possibile e di solito viene selezionata la finestra di Hanning. Dal dominio del tempo, l'aggiunta della finestra di Hanning rende effettivamente 0 la fase del punto iniziale e del punto finale del segnale di campionamento periodico, superando il fenomeno per cui la fase del segnale di campionamento è discontinua all'inizio e alla fine a causa delle fluttuazioni di frequenza , ma qualsiasi funzione della finestra non può risolvere l'errore causato dalla deviazione del punto zero nel lobo principale, quindi anche la riduzione delle perdite è limitata. La tecnologia di interpolazione può eliminare quasi completamente l'influenza della perdita, ma il volume di elaborazione dei dati di questo algoritmo è troppo grande e le prestazioni in tempo reale sono difficili da garantire. La letteratura propone un algoritmo per ridurre la perdita di spettro. Il suo nucleo è che quando il prodotto del periodo di campionamento e il numero di punti di campionamento è uguale a un multiplo intero del periodo del segnale, la sequenza discreta ottenuta dall'algoritmo è la sequenza di campionamento del segnale. In caso contrario, l'algoritmo regolerà automaticamente il campionamento. sequenza. La simulazione dimostra che l'algoritmo migliora la dispersione dello spettro in modo più evidente quando la fluttuazione della frequenza del segnale non è grande e la precisione dell'algoritmo è inferiore quando la fluttuazione della frequenza del segnale è grande. La caratteristica generale dell'algoritmo di cui sopra è correggere la sequenza di campionamento o lo spettro di frequenza, senza risolvere la causa principale della perdita di spettro. Ciò determina che l'algoritmo o l'effetto di cui sopra non è significativo o che le prestazioni in tempo reale sono scarse. La causa principale della perdita di spettro è fs≠Nf0. Solo regolando fs in tempo reale per rendere fs=Nf0 è possibile risolvere efficacemente la perdita di spettro. Sulla base dello scopo di cui sopra, viene proposto un algoritmo per regolare in modo adattativo la frequenza di campionamento e la simulazione dimostra l'efficacia dell'algoritmo.
Il fattore principale che influenza la velocità di questo algoritmo è FFT. Negli ultimi anni, con l'emergere di chip DSP particolarmente adatti per l'elaborazione dei dati e le loro applicazioni nell'analisi periodica del segnale, le operazioni FFT sono diventate sempre più veloci. L'utilizzo di VC5402 per eseguire operazioni FFT complesse a 1024 punti richiede solo 40 μs, ovvero completamente soddisfacente. Requisiti di sistema in tempo reale. Pertanto, questo algoritmo ha un forte valore pratico nel sistema basato sulla misurazione del segnale CA. L'algoritmo è attualmente applicato alla progettazione del sistema di monitoraggio delle centrali idroelettriche.
Perdita di spettro nella profilometria in trasformata di Fourier
La profilometria in trasformata di Fourier (FTP) è un metodo di misurazione della superficie tridimensionale comunemente usato. Il suo principio di funzionamento è costituito dalle seguenti tre parti: 1) La forma della superficie dell'oggetto tridimensionale in prova modula spazialmente il campo di luce strutturato del reticolo, in modo che il campo di luce strutturato deformato porti l'informazione della distribuzione in altezza dei tre -forma dimensionale della superficie; 2) Per la distribuzione continua Il campo di luce strutturato deformato viene campionato per ottenere informazioni discrete per una facile elaborazione al computer; 3) Il computer esegue la trasformata di Fourier sulle informazioni discrete ottenute, seleziona una finestra di filtro appropriata per filtrare la componente di frequenza fondamentale dallo spettro e inverte la componente di frequenza fondamentale. La trasformata di Fourier ripristina la distribuzione in altezza della superficie misurata.
Quando la trasformata di Fourier viene eseguita sul campo di luce strutturata deformata discreta, l'algoritmo della trasformata discreta di Fourier richiede l'espansione periodica del campo di luce strutturata deformata nel dominio dello spazio. L'estensione del periodo può causare perdite di spettro, quindi verranno introdotti errori nella misurazione della profilometria della trasformata di Fourier, ma poche persone ne discutono teoricamente. Al fine di ridurre la perdita di spettro causata dall'espansione del periodo, le persone spesso scelgono una funzione finestra appropriata (come la finestra Hanning) per pesare il campo luminoso deformato, in modo che il campo luminoso deformato campionato dal CCD venga elaborato dalla funzione finestra e il l'intensità del bordo della finestra è 0, quindi la trasformata di Fourier. Tuttavia, dopo che il segnale è stato elaborato dalla funzione finestra, alcune informazioni andranno perse, il che equivale a ridurre la perdita di spettro introducendo anche errori. Questo articolo analizza il problema della perdita di spettro del campo luminoso deformato con spazio limitato. La relazione tra il periodo esteso e la dispersione dello spettro del campo ottico della struttura deformata viene teoricamente dedotta e vengono forniti il metodo di calcolo e l'analisi quantitativa dell'errore. Si fa notare che solo quando il periodo di espansione è uguale ad un multiplo intero del periodo del reticolo, le frange espanse sono continue, e la trasformata di Fourier non provoca dispersione di spettro; quando il periodo di espansione non è uguale a un multiplo intero del periodo del reticolo, le frange espanse sono discontinue. Soprattutto quando c'è una differenza di 0,5 del periodo del reticolo tra il periodo di espansione e il multiplo intero del periodo del reticolo del campo luminoso deformato, la rottura della frangia è la più grave dopo l'espansione e la perdita dello spettro è la più grande. Pertanto, quando si misura con la profilometria in trasformata di Fourier, provare a scegliere il periodo di espansione uguale a un multiplo intero del periodo del segnale per ridurre l'errore di misura causato dalla dispersione dello spettro. Se ciò non è possibile, è possibile utilizzare un metodo iterativo per estrapolare le frange per generare nuove frange su entrambi i lati del campo visivo effettivo per estendere l'errore di perdita oltre il campo visivo effettivo e ridurre l'errore di perdita dal bordo.
