Quaestio Introductio
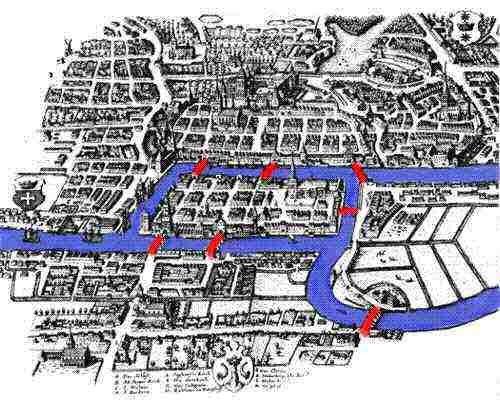
XVIII secolo dei Gobini, c'è un fiume che attraversa, ci sono due isole, ci sono sette ponti che collegano due isole con la riva del fiume (come mappa di contorno). Alcune persone hanno proposto una domanda: come può un pedone non ripetere, non perdere i sette ponti alla volta e tornare finalmente al punto di partenza. Successivamente, il grande matematico Euli lo trasformò in un problema geometrico, un problema pittorico. Non solo ha risolto questo problema, ma fornisce anche un riempimento di un grafico di un'immagine: il numero di punti dispari non è 0 è 2 (anche il numero di numeri dispari ", se è Il numero pari è chiamato pari. Se tu vuoi disegnare un'immagine, devi avere una cosa uniforme nel mezzo, cioè c'è un altro modo per avere un altro modo, e la singolarità può essere solo su entrambe le estremità, quindi qualsiasi figura può essere disegnata, Hai avuto o su entrambe le estremità).
Consequentia modum
Quando l'Eulero visitò la Gobisburg prussiana (ora Russia Galoningrad), trovò un pubblico locale molto interessante. Confuciare. C'è un fiume chiamato Pregel a Gobinic City, questo passatempo interessante è una passeggiata da tutti e sette i ponti il sabato, e ogni ponte può passare solo una volta e il punto di partenza deve essere lo stesso posto. .
Euchi mette ogni pezzo in un punto, collegando due ponti terrestri.
È impossibile indagare in questo modo. La sua argomentazione è questa, eccetto per il punto di partenza, ogni volta che una persona entra in una terra (o punto) da un ponte, lascerà anche questo punto da un altro ponte. Pertanto, ogni linea si trova in un punto, due ponti (o linee) vengono calcolati dalla linea dal punto di partenza e dalla linea dell'ultimo punto di ritorno, quindi il numero di ponti collegati ad altre terre è quasi pari.
Difficultas est
Seven bridge, non c'è punto contenente il numero di orientamenti, quindi le attività di cui sopra non possono essere completate.
Eulero è molto importante, è anche molto intelligente, sta dimostrando l'unicità del matematico che si occupa di problemi pratici - astrae un problema reale in un "modello matematico" adatto. Questo metodo di ricerca è "Metodo del modello matematico". Questo non ha bisogno di usare quanto profonda teoria, ma pensa a questo, ma alla chiave per risolvere il problema.
Successivamente, Eulero usa un dipinto nella figura per giudicare le linee guida e giudica rapidamente che i 7 ponti che non ripetono il porto di Doinsburg una volta. In altre parole, quanti anni vengono, le persone prestano attenzione al percorso non ripetitivo, non esistono affatto. Un problema che è stato difficile da vivere, in realtà è una risposta così scarna!
Finalis factum
Il periodo iniziale del problema
Dopo che la domanda è stata sollevata, molte persone sono molto interessate a questo, ma stanno sperimentando, ma per molto tempo non sono mai stato risolto. Con la normale conoscenza matematica, ogni ponte viene preso una volta e tutti e sette i ponti percorrono un totale di 5040, e così tanti casi, sarà un processo, il che richiederà molto carico di lavoro. Ma come posso trovare un percorso che attraversi con successo ogni ponte invece di ripetere? Pertanto, si forma un famoso "problema dei sette ponti di Gossoburg".
Problema Post-esposizione
1735, ci sono diversi studenti universitari che scrivono una lettera al geniale matematico Eura, che lavora in Russia, l'Accademia delle scienze di Porsopian. Chiedigli di aiutarti a risolvere questo problema. Ou stava osservando l'Hard Bridge nel Gobi, pensandoci seriamente, ma non era riuscito ad avere successo, quindi sospettava che la questione Qiqiao non lo risolvesse?
Nel 1736, dopo un anno di ricerche, Orap, 29 anni, presentò i documenti del "Gobi Seven Bridge", risolse con successo questo problema e creò una nuova branca della matematica: la teoria dei grafi.
Nel documento, Eutu astrarrà la questione Qiqiao e prenderà ogni pezzo in un punto, collegando due ponti terrestri. E quindi ha ottenuto la stessa geometria mostrata. Se usiamo A, B, C, D quattro punti per rappresentare le quattro aree di Gobinic. Un così famoso "problema dei sette ponti" viene convertito nella possibilità di utilizzare un dipinto non ripetitivo delle sette linee. Se sai disegnare, devi avere punti finali e punti iniziali nella grafica, e il punto iniziale e il punto finale dovrebbero essere gli stessi. Poiché la simmetria può essere vista da B o C come punto di partenza, se si presume che A sia il punto di partenza e il punto finale, allora deve essercene uno lontano dal filo e dalla riga di ingresso corrispondente. Se definiamo il numero di righe della linea che entra in A, il numero di righe che escono dal filo è l'uscita e il numero di aste della linea è un grado di A, quindi a Il grado e il grado di gradi sono uguali, cioè, il grado di A dovrebbe essere un numero pari. Cioè, è necessario prendere un decisore da A. La degilità della degilità dovrebbe essere un numero pari, e il grado di effettivamente A è 5 è dispari, quindi si può vedere che non è subordinabile da A. Allo stesso tempo, se è da B o D, poiché B, i gradi di D sono 3, 3, ognuno è dispari, cioè il punto di partenza è inedito.
È noto che il motivo di cui sopra è che il problema matematico astratto non è subalipato, cioè anche il "problema dei sette ponti" è inedito.
From this we get: Euler loop relationship
Quindi possiamo sapere che un grafico può essere disegnato, deve soddisfare le seguenti due condizioni:
1. La grafica deve essere collegata.
2. Il numero di "quote" nella figura è 0 o 2.
Possiamo anche verificare che la grafica possa essere disegnata. Può anche essere giudicato per giudicare i "sette problemi di bridge", 4 punti sono dispari, può sapere che l'immagine non può essere "disegnata", cioè non è possibile passare ripetutamente tutti e sette i ponti.
Nel 1736 Eucula spiegò il suo metodo risolutivo nelle Carte del "Ponte Gobinburg 7", che fu consegnato all'Accademia di Pietroburgo. La sua induzione, ponendo le basi per il nuovo ramo matematico: l'istituzione della topologia.
Domanda di Qiqiao e teorema di Eulero
Eulero adotta la ricerca sulla questione Qiqiao, non solo per replicare il problema proposto dai residenti di Gobinburg E ha ottenuto e dimostrato tre conclusioni relative a un ictus, e le persone sono spesso chiamate il teorema di Eulero. Per una mappa di collegamento, di solito viene chiamata Strada di Eulero da un percorso tracciato da un nodo. Le persone di solito chiamano una coppia di circuiti di Eulero che vengono riportati al punto di partenza. Un'immagine con il ciclo europeo è chiamata mappa di Eulero.
Questo argomento è incluso nel 12 ° libro della Matematica Matematica. 104 pagine.
Questo argomento è incluso anche nel primo volume del primo volume. A pagina 121.
Un dipinto
⒈⒈⒈ ⒈ 通 通 通 图 图 图 图 图 图 图 图 图 图 图 通 图 图 图 图 图 图 图When you draw, you can take anything at the starting point, and finally you can draw this picture with this point.
⒉ Ubi duo tantum prospectus impar (cetera par est), ducenda est. Cum ducatur, oportet punctum extraneum ponere ut principium, et aliud punctum impar est finis.
⒊ Aliae status tabulae haurire non possunt. (Numerus punctorum imparium computari potest in secunda figura ut paucas partes trahat).
