Историјска позадина
Више од пола века пре него што је Максвел рођен, људи су направили велики напредак у разумевању електромагнетних појава. Године 1785. француски физичар Ц. А. Цоуломб (Цхарлес А. Цоуломб) успоставио је Кулонов закон који описује силу интеракције између два тачкаста наелектрисања на основу резултата експеримента торзијске равнотеже. Године 1820, Х. Ц. Оерстед (Ханс Цхристиан Оерстед) је открио да електрична струја може да одбије магнетне игле, повезујући тако електрицитет са магнетизмом. Након тога, А. М. Ампер (Андре Марие Ампере) је проучавао интеракцију између електричних струја и изнео многе важне концепте и закон Амперове петље. М. Фарадеј (Мајкл Фарадеј) дао је изузетан допринос у многим аспектима, посебно у закону електромагнетне индукције објављеном 1831. године, који је важна теоријска основа за моторе, трансформаторе и другу опрему.
Године 1845, три најосновнија експериментална закона о електромагнетним појавама: Кулонов закон (1785), Биот-Савартов закон (1820), Фарадејев закон електромагнетне индукције (1831 ~ 1845) сумирани су, Фарадејев концепт за " и "линија магнетне силе" (сада се називају и "линија електричног поља" и "линија магнетне силе") су развијене у "концепт електромагнетног поља". Од 1855. до 1865. Максвел је свеобухватно прегледао Кулонов закон, Биот-Савартов закон и Фарадејев закон и донео методе математичке анализе у поље електромагнетних истраживања, што је довело до рађања Максвелове електромагнетне теорије. .
Пре Максвела, све теорије о електромагнетним појавама биле су засноване на концепту дејства преко раздаљине. Веровало се да се интеракција између наелектрисаних тела, магнетизованих тела или проводника са струјом може извршити директно изван средњег медијума. И то се ради одмах, односно брзина ширења електромагнетног поремећаја се сматра бесконачном. У то време само је Фарадеј имао другачија мишљења. Он сматра да су наведене интеракције везане за посредне медије и да се одвијају кроз трансфер посредних медија, односно заговарајући теорију индиректног трансфера.
Максвел је наследио Фарадејево гледиште, осврнуо се на модел механике флуида, применио ригорозне математичке форме да сумира рад претходника, предложио хипотезу о струји померања, проширио значење струје и закључио основне законе електромагнетног поља. четири диференцијалне једначине, које су познате Максвелове једначине. Он је анализирао овај скуп једначина, предвиђајући постојање електромагнетних таласа, и закључио да је брзина простирања електромагнетних таласа коначна вредност (близу брзини светлости), а да је и светлост електромагнетни талас одређене фреквенције. Све наведено је написао у свом раду под насловом „О електрицитету и магнетизму“.
Године 1887. Хајнрих Р. Херц је користио експерименталне методе за генерисање и детекцију електромагнетних таласа, што је потврдило Максвелово предвиђање. Између 1905. и 1915. године, теорија релативности Алберта Ајнштајна је даље демонстрирала однос између времена, простора, масе, енергије и кретања, указујући да су електромагнетна поља облик материје, а теорија индиректности је призната.
Састав једначине
Максвелове једначине се састоје од четири једначине:
Гаусов закон: Овај закон описује однос између електричног поља и расподеле наелектрисања у простору. Линије електричног поља почињу позитивним наелектрисањем и завршавају се негативним наелектрисањем (или бесконачно). Израчунајте број линија електричног поља које пролазе кроз дату затворену површину, односно њен електрични флукс, и можете сазнати укупно наелектрисање садржано у овој затвореној површини. Детаљније, овај закон описује однос између електричног флукса који пролази кроз произвољну затворену површину и наелектрисања у затвореној површини.
Гаусов магнетни закон: Овај закон показује да магнетни монополи заправо не постоје. Дакле, нема изолованог магнетног набоја, а линија магнетног поља нема почетну и крајњу тачку. Линије магнетног поља ће се запетљати или проширити до бесконачности. Другим речима, линије магнетног поља које улазе у било коју област морају напустити то подручје. У терминологији, магнетни флукс који пролази кроз било коју затворену површину једнак је нули, или је магнетно поље пасивно поље.
Фарадејев закон индукције: Овај закон описује како временско променљиво магнетно поље индукује електрично поље. Електромагнетна индукција је теоријска основа за производњу многих генератора. На пример, магнет са ротирајућим шипкама генерише временски променљиво магнетно поље, које заузврат генерише електрично поље, узрокујући да суседно затворено коло индукује струју.
Максвел-Амперов закон: Овај закон каже да се магнетно поље може генерисати на два начина: један је провођењем струје (оригинални Амперов закон), а други је временски променљивим електричним пољем, или струјом померања (Максвелов термин корекције) .
У електромагнетици, Максвелов термин корекције значи да електрично поље које се мења у времену може да генерише магнетно поље, а због Фарадејевог закона индукције, временско променљиво магнетно поље може да генерише електрично поље. На овај начин, две једначине теоретски дозвољавају да се самоодрживи електромагнетни таласи шире у свемиру.
Главне тачке Максвелове теорије електромагнетног поља могу се сажети на следећи начин:
①Неколико дискретних наелектрисаних објеката или струја, све електричне и магнетне интеракције између њих се преносе између њих. Оно што се преноси у средњем делу, без обзира да ли је средња област вакуум или физичка супстанца.
②Електрична енергија или магнетна енергија не постоји само у наелектрисаним телима, магнетизованим телима или наелектрисаним објектима, већ се највећи део дистрибуира у околном електромагнетном пољу.
③Ако дође до прекида у колу које формира проводник, струја проводљивости у колу ће бити компензована струјом померања у диелектрику, то јест, пуна струја је континуирана. А однос између струје померања и магнетног поља које генерише је исти као код струје проводљивости.
④ Магнетни флукс нема ни почетак ни крај, односно нема магнетног наелектрисања.
⑤Светлосни таласи су такође електромагнетни таласи.
Постоје два начина да се изразе Максвелове једначине.
1. Интегрални облик Максвелових једначина је математички модел који описује електромагнетно поље у одређеној запремини или области. Израз је:
Equation ① is the law of total current derived from the generalization of the law of Ampere’s loop, and its meaning is: the line integral of the magnetic field intensity H along any closed curve is equal to the area passing through the limited area of this curve Full current. The first term on the right side of the equal sign is the conduction current. The second term is the displacement current. Equation ② is the expression of Faraday's law of electromagnetic induction, which shows that the line integral of the electric field intensity E along any closed curve is equal to the negative value of the rate of change of the magnetic flux passing through the area defined by the curve with respect to time. The closed curve mentioned here does not necessarily have to be composed of conductors, it can be a dielectric loop, or even just any closed contour. Equation ③ represents the principle of magnetic flux continuity, indicating that for any closed curved surface, as much magnetic flux enters the curved surface, the same amount of magnetic flux leaves. That is to say, the B line has neither a beginning nor a terminal; it also shows that there is no magnetic charge corresponding to the electric charge. Equation ④ is the expression of Gauss's law, which shows that under time-varying conditions, the net flux of D from any closed surface should be equal to the sum of all free charges in the volume enclosed by the closed surface.
2. Максвелове једначине у диференцијалном облику. Диференцијални облик Максвелових једначина је за сваку тачку у пољу. Користећи дел оператор, они се могу написати као
Једначина ⑤ је диференцијални облик закона укупне струје, који показује да је завој интензитета магнетног поља Х једнак укупној густини струје у овој тачки (густина струје проводљивости Ј и густина струје померања Тхе збир), тј. извор вртлога магнетног поља је пуна густина струје, а струја померања може да генерише магнетно поље баш као и струја проводљивости. Формула ⑥ је диференцијални облик Фарадејевог закона електромагнетне индукције, који показује да је завој интензитета електричног поља Е једнак негативној вредности временске брзине промене густине магнетног флукса Б у овој тачки, тј. вортексни извор електричног поља је временска брзина промене густине магнетног флукса. Једначина ⑦ је диференцијални облик принципа континуитета магнетног флукса, који показује да је дивергенција густине магнетног флукса Б увек једнака нули, односно да Б линија нема почетак и крај. То значи да не постоји магнетни набој који одговара електричном наелектрисању. Једначина ⑧ је генерализација Гауссовог закона електростатичког поља, то јест, под временским променљивим условима, дивергенција електричног померања Д је и даље једнака густини слободног наелектрисања у овој тачки.
Поред горње четири једначине, потребан је и конститутивни однос медијума
да се коначно реши проблем решавања квантитета поља. Где је ε диелектрична константа средине, μ је пермеабилност средине, а σ проводљивост средине.
Форма израза
Интегрални облик
Интегрални облик Максвелових једначина је следећи:
Ово је 1873. Око године Максвел је предложио четири једначине које изражавају универзални закон електромагнетних поља. Међу њима:
(1) описује природу електричног поља. Уопштено говорећи, електрично поље може бити електрично поље слободног наелектрисања или индуковано електрично поље побуђено променљивим магнетним пољем, а индуковано електрично поље је вртложно поље, а његова електрична линија померања је затворена и не доприноси флуксу затворене закривљене површине.
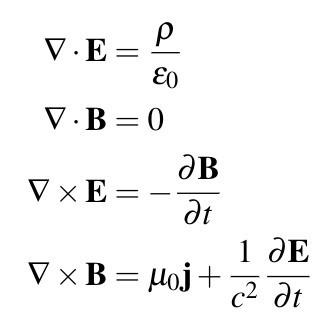
(2) описује природу магнетног поља. Магнетно поље може бити побуђено струјом проводљивости или струјом померања променљивог електричног поља. Њихова магнетна поља су све вртложна поља, а линије магнетне индукције су затворене линије, које не доприносе флуксу затворене закривљене површине.
(3) описује закон променљивог магнетног поља да побуђује електрично поље.
(4) описује закон провођења струје и промену електричног поља да би се побуђивало магнетно поље.
Форма у стабилном пољу
Када
, једначине се своде на једначине електростатичког поља и стационарног магнетног поља :
Образац у слободном простору без извора поља
Када, the equation system becomes the following form:
The integral form of Maxwell's equations reflects the relationship between the amount of electromagnetic field (D, E, B, H) and the field source (charge q, current I) in a certain area of space.
Диференцијални облик
У стварној примени електромагнетног поља, често је потребно знати однос између количине електромагнетног поља тачку по тачку у простору и наелектрисања и струје. Из математичке форме, интегрални облик Максвелових једначина се трансформише у диференцијални облик. Обрнути троугао је Хамилтонов.
Белешка:
(1) У различитим инерцијалним референтним системима Максвелове једначине имају исти облик.
(2) Да би се примениле Максвелове једначине за решавање практичних проблема, мора се узети у обзир и утицај средине на електромагнетно поље. На пример, у униформној и изотропној средини, количина електромагнетног поља има следећу везу са карактеристикама средине:
У неуједначеној средини, граничну вредност количине електромагнетног поља на интерфејсу такође треба сматрати Односом. Користећи услов почетне вредности величине поља када је т=0, у принципу се може добити електромагнетно поље у било којој тачки простора у било ком тренутку, односно Е(к, и, з, т) и Б(к, и, з т).
Следе Максвелове једначине под Гаусовим системом јединица
Једначине физичких својстава
Када there is a medium, due to electric and magnetic fields The interaction with the medium makes the amount of electromagnetic field related to the characteristics of the medium. Therefore, the above-mentioned Maxwell equations are not complete at this time, and the physical property equations describing the properties of the medium (isotropic medium) need to be supplemented, respectively
У формули, ε, μ и σ су апсолутна диелектрична константа, апсолутна пермеабилност и проводљивост проводника, односно брзина.
Даљи теоријски доказ да су Максвелове једначине и једначине физичких својстава заједно комплетан скуп једначина за одређивање промена електромагнетног поља. Односно, када се дају наелектрисање и струја, промена електромагнетног поља се може у потпуности одредити из горње једначине према почетним условима (и неопходним граничним условима). Наравно, ако желите да разговарате о утицају електромагнетног поља на наелектрисане честице и кретању наелектрисаних честица у електромагнетном пољу, потребна вам је и формула Лоренцове силе.
Форма комплексног броја
За синусоидна временски променљива поља, комплексни вектори се могу користити да се закон електромагнетних поља изрази као комплексни бројеви.
У комплексном закону електромагнетног поља, пошто су комплексна величина поља и изворна величина само функције положаја простора, при решавању је непотребно разматрати њихову зависност од времена. Због тога је погодније користити сложени закон електромагнетног поља за дискусију о синусоидном пољу које се мења у времену.
Примедбе
Користећи различите системе јединица, облик Максвелових једначина ће бити мало промењен, а општи облик је и даље исти, али ће се различите константе појавити на различитим позицијама унутар једначине.
Међународни систем јединица је најчешће коришћени систем јединица. Цела област инжењерства користи овај систем јединица. Већина хемичара такође користи овај систем јединица. Скоро сви уџбеници физике на факултетима користе овај систем јединица. Систем. Други често коришћени системи јединица су Гаусс, Лорентз-Хеависиде јединице и Планцк. Гаусов систем јединица изведен из система центиметар-грам-секунда је погоднији за наставне сврхе и може учинити да једначине изгледају једноставније и лакше разумљиве. Систем јединица Лоренц-Хевисајд је такође изведен из система центиметар-грам-секунда и углавном се користи у физици честица; Планков систем јединица је природни систем јединица, а његове јединице су дефинисане према природи природе. Поставио човек. Планков систем јединица је веома користан алат за проучавање теоријске физике и може дати велико просветљење. На овој страници, осим ако није другачије назначено, све једначине су у Међународном систему јединица.
Овде су приказана два еквивалентна израза Максвелових једначина. Први израз је следећи:
Овај израз додаје слободно наелектрисање и везано наелектрисање укупном наелектрисању које захтева Гаусов закон, а такође дели слободну струју, везану струју и струју поларизације. Укупни износ је укупна струја у Максвел-Амперовом закону. Овај израз усваја релативно основно и микро гледиште. Овај израз се може применити за израчунавање електричних и магнетних поља генерисаних коначним наелектрисањем извора и изворном струјом у вакууму. Међутим, у стварности има превише електрона и атомских језгара у материји који се не могу укључити у прорачун. У ствари, класичном електромагнетизму нису потребни тако прецизни одговори.
За други израз, молимо вас да погледате „општи облик“ у горе поменутом „обрасцу интеграције“. Узима слободно наелектрисање и слободну струју као извор и не израчунава директно допринос везаног наелектрисања који се појављује у диелектрику и везане струје и струје поларизације која се појављује у магнетизованој супстанци. Пошто у општим стварним условима, параметри који се могу директно контролисати су слободно наелектрисање и слободна струја, а везано наелектрисање, везана струја и струја поларизације су појаве које се јављају након поларизације супстанце. Коришћење овог израза ће учинити диелектричност или магнетизацију Различити физички прорачуни унутар супстанце су лакши.
На површини се чини да су Максвелове једначине претерано одређене. Има само шест непознатих (векторско електрично поље и магнетно поље имају по три непознате, струја и наелектрисање нису непознате. То је физичка величина која се слободно поставља и одговара очувању наелектрисања), али постоји осам једначина (две Гаусове закони имају две једначине, Фарадејев закон и Амперов закон су векторски, од којих свака садржи три једначине). Ова ситуација је повезана са ограниченом поновљивошћу Максвелових једначина. Из теорије се може закључити да сваки систем који задовољава Фарадејев закон и Амперов закон мора да задовољи два Гаусова закона.
С друге стране, Максвелове једначине нису затворене. Само с обзиром на карактеристике електромагнетне средине, овај систем једначина може добити дефинитивно решење.
Применљива скала
The Maxwell equations are usually applied to the "macro average field" of various fields. Када the scale shrinks to the microscopic scale, so as to approach the size of a single atom, the local fluctuations of these fields will become unignorable, and quantum phenomena will begin to appear. Only under the premise of macro-average, some physical quantities such as the permittivity and permeability of a substance can get meaningful definition values.
Полупречник најтежег језгра је око 7 фемтометара (1фм=10-15м). Дакле, у класичној електромагнетици, микроскопска скала се односи на ред величине већи од 10-14м. Да би се задовољила микроскопска скала, електрони и језгра се могу сматрати тачкастим наелектрисањем, а микроскопске Максвелове једначине су успостављене; иначе се мора узети у обзир расподела наелектрисања унутар језгра. Електрично и магнетно поље израчунато на микроскопској скали се и даље прилично драстично мења, растојање просторне промене је мање од 10-10м, а период промене времена је између 10-17 и 10-13 секунди. Стога, из микроскопских Максвелових једначина, мора се извршити класична операција усредњавања да би се добило глатко, континуирано и полако променљиво макроскопско електрично поље и макроскопско магнетно поље. Најнижа граница макро скале је 10-8 метара. То значи да се понашање рефлексије и преламања електромагнетних таласа може описати макро-Максвеловим једначинама. Узимајући ову минималну границу као дужину странице, коцка запремине 10-24 кубна метра садржи приближно 106 језгара и електрона. Физичко понашање толиког броја језгара и електрона, након класичног усредњавања, довољно је да изглади све насилне флуктуације. Према поузданим литературним записима, класична операција усредњавања захтева само усредњавање у простору, а не у времену, и не мора да узме у обзир квантне ефекте атома.
Значај
Максвелов допринос стварању концепта поља је такође велика иновација у физици тог времена, јер је управо појава концепта поља учинила да су многи научници успели да се ослободе окова Њутновог „концепта супер-дистанце“ и опште прихваћена идеја да су и електромагнетни и гравитациони ефекти „близина“.
Положај Максвелових једначина у електромагнетици и класичној електродинамици је исти као положај Њутнових закона кретања у Њутновој механици. Електромагнетна теорија усредсређена на Максвелове једначине једно је од најпоноснијих достигнућа класичне физике. Савршено јединство електромагнетне интеракције које је открило успоставило је уверење за физичаре да различите интеракције материје треба да буду уједињене на вишем нивоу. Ова теорија се широко примењује у техничким областима.
Научни значај
(1) Класичну теорију поља је утемељио Максвел крајем 19. века на основу сумирања три експериментална закона електромагнетике и поређења са механичким моделима. Али, Максвелово главно достигнуће му је управо омогућило да се извуче из оквира класичне механике: у физици је узео „поље” уместо „сила” као основни објекат истраживања и увео векторску делимичну диференцијалну операцију која се разликује од класична математика у математици. Симбол. Ова два су основа за откриће једначине електромагнетног таласа. Односно, Максвелов рад је заправо пробио оквире класичне физике и математике у то време, али због историјских услова у то време, људи још увек могу да разумеју теорију електромагнетног поља само из оквира Њутновог рачуна и класичне механике. .
Савремена математика, математичка анализа у Хилбертовом простору појавила се тек на прелазу из 19. у 20. век. Концепт таласа материје у квантној механици откривен је касније, посебно нераскидива математичка логичка веза између модерне математике и квантне физике још увек није у потпуности схваћена и прихваћена од стране људи. Од Максвеловог успостављања теорије електромагнетног поља до данас, људи су увек користили класичну математику у Еуклидском простору као основни метод за решавање Максвелових једначина.
(2) Из појаве, форме, садржаја и историјског процеса Максвелових једначина, можемо видети: Прво, физички објекат се развија у нови аксиомски израз на дубљем нивоу. Будући да га човечанство овлада, научни напредак неће еволуирати под утврђеним претпоставкама. Успостављање новог система аксиома са когнитивним значајем знак је научно-теоријског напретка. Друго, иако су физички објекат и начин његовог изражавања различите ствари, немогуће је препознати „постојање“ овог објекта без ослањања на одговарајући метод изражавања. Треће, теорија коју градимо одредиће ниво значења у којем своје објекте чинимо физичким чињеницама. Управо то је конфузија коју нам је донела модерна најсавременија физика.
(3) Максвелове једначине откривају лепоту симетрије у међусобној трансформацији електричног и магнетног поља. Ова лепота је у потпуности изражена у модерном математичком облику. Међутим, с једне стране, треба признати да само одговарајућа математичка форма може у потпуности показати интегритет (електромагнетну симетрију) који се не може видети у емпиријском методу; с друге стране, не треба заборавити да је лепота ове симетрије у математичком облику. Одразила се јединствена природа електромагнетног поља. Стога, треба да схватимо да ову симетрију треба да „откријемо“ или „видимо“ у математичким изразима, а не да директно изводимо ову суштину из физичких математичких формула.
