Backgroundscientia
TheID3algorithmwasfirstproposedbyJ.RossQuinlanattheUniversityofSydneyin1975asaclassificationpredictionalgorithm.Thecoreofthealgorithmis"informationentropy"..TheID3algorithmcalculatestheinformationgainofeachattributeandconsidersthattheattributewithhighinformationgainisagoodattribute.Eachtimetheattributewiththehighestinformationgainisselectedasthepartitionstandard,thisprocessisrepeateduntiladecisiontreethatcanperfectlyclassifytrainingexamplesisgenerated.
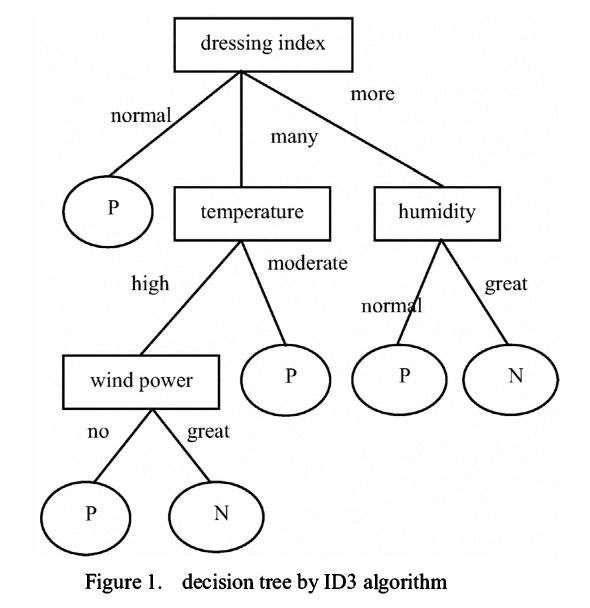
Decisiontreeistoclassifydatatoachievethepurposeofprediction.Thedecisiontreemethodfirstformsadecisiontreebasedonthetrainingsetdata.Ifthetreecannotgivethecorrectclassificationtoallobjects,selectsomeexceptionstoaddtothetrainingsetdata,andrepeattheprocessuntilthecorrectdecisionsetisformed.Thedecisiontreerepresentsthetreestructureofthedecisionset.
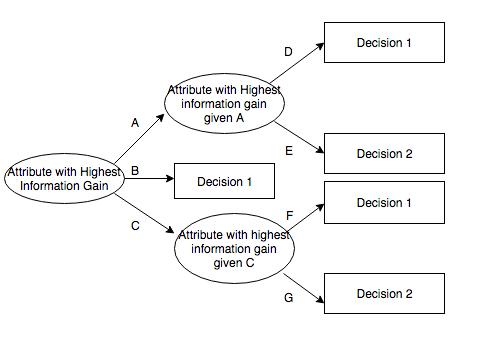
Thedecisiontreeiscomposedofdecisionnodes,branchesandleaves.Thetopnodeinthedecisiontreeistherootnode,andeachbranchisanewdecisionnode,oraleafofthetree.Eachdecisionnoderepresentsaproblemordecision,andusuallycorrespondstotheattributesoftheobjecttobeclassified.Eachleafnoderepresentsapossibleclassificationresult.Intheprocessoftraversingthedecisiontreefromtoptobottom,eachnodewillencounteratest,andthedifferenttestoutputsoftheproblemoneachnodewillleadtodifferentbranches,andfinallyaleafnodewillbereached.ThisprocessItistheprocessofusingdecisiontreestoclassify,usingseveralvariablestodeterminethecategoryitbelongsto.
ID3algorithm
TheID3algorithmwasfirstproposedbyQuinlan.Thealgorithmisbasedoninformationtheory,andusesinformationentropyandinformationgainasmeasurementstandards,soastorealizetheinductiveclassificationofdata.Thefollowingaresomebasicconceptsofinformationtheory:
Definitio1: If therearenmessages with the sameprobability, theprobability pofeachmessageis1/n, and the amount ofinformationtransmitted by amessageis-Log2(1/n)
Definitio2: Si sunt in- scriptiones, et datae sunt probabilitatisdistributionisP=(p1,p2...pn), ergo summa informationes transmissae per thedistributionem dictae entropyofP.
.
Definition3: Ifare cordsetTis dividedin to independentcategories C1C2..Ckaccording to the value of the praedica- goryattribute, the amount ofinformationeeded toidentify which categoryanementoft belongstoisInfo(T)=I(p),ubi Pistheprobabilitas distribuendi C1C2./(|)C1|, P=(|)Ck|
Definition4:IfWefirstdivideTintosetsT1,T2...Tnaccordingtothevalueofthenon-categoryattributeX,andthendeterminetheamountofinformationofanelementclassinTcanbeobtainedbydeterminingtheweightedaveragevalueofTi,thatis,theweightedaveragevalueofInfo(Ti)is:
Info(X,T)=(i=1tonsum)((|Ti|/|T|)Info(Ti))
Definition5:InformationGainisthedifferencebetweentwoamountsofinformation.OneamountofinformationistheamountofinformationofoneelementofTthatneedstobedetermined,andtheotheramountofinformationistheamountofinformationofoneelementofTthatneedstobedeterminedafterthevalueofattributeXhasbeenobtained.Theinformationgaindegreeformulais:
Quaestum(X,T)=Info(T)-Info(X,T)
ID3algorithmcalculatestheinformationgainofeachattribute,Andselecttheattributewiththehighestgainasthetestattributeofthegivenset.Createanodefortheselectedtestattribute,markitwiththeattributeofthenode,createabranchforeachvalueoftheattributeanddividethesampleaccordingly.
Datadescription
Thesampledatausedhascertainrequirements.ID3is:
Description-attribute-attributeswiththesamevaluemustdescribeeachexampleandhaveafixednumberofvalues.
Pre-definedclass-instanceattributes must have been ended, that, they are notlearnedID3.
Discreteclass-theclassmusthesharpanddistinct.Thedecomposition ofcontinuousclassesintofuzzycategories (ut metalla esse "durum, difficile, flexibile, mansuetum et molle" non est credibile.
Enoughexamples-becauseinductivegeneralizationisusedfor(Thatis,itisnotpossibletofindout.)Enoughtestcasesmustbeselectedtodistinguishvalidpatternsandeliminatetheinfluenceofspecialcoincidencefactors.
Attributeselection
ID3determineswhichattributesarebest.Astatisticalfeature,calledinformationgain,usesentropytoobtainagivenattributetomeasurethetrainingexamplesbroughtintothetargetclass.Theinformationwiththehighestinformationgain(informationisthemostusefulcategory)isselected.Inordertoclarifythegain,wefirstborrowfrominformationtheoryOnedefinitioniscalledentropy.Everyattributehasanentropy.
