1. Meaning
Codice di ridondanza del ciclo, noto anche come codice di stile plurale. Il metodo di lavoro del CRC consiste nel generare un codice di ridondanza all'estremità trasmittente e le informazioni vengono inviate all'estremità ricevente insieme e le informazioni ricevute dall'estremità ricevente vengono verificate dallo stesso algoritmo nell'estremità trasmittente, se l'errore viene trovato, quindi notificare al mittente la ritrasmissione.
Nel campo della memorizzazione dei dati e della comunicazione dei dati, al fine di garantire che i dati corretti siano corretti, è necessario utilizzare i mezzi di rilevamento degli errori. In molti mezzi sbagliati, CRC è il più famoso. Le sue caratteristiche sono: codificatore e circuito di rilevamento estremamente rilevati, piccolo overhead, facile da usare. Dalla sua capacità di rilevamento degli errori, la possibilità di errori che non può essere trovata è solo dello 0,0047% o meno. Dal punto di vista delle prestazioni e dell'overhead, è molto meglio della parità, dell'aritmetica e del controllo. Pertanto, nel campo dell'archiviazione e della comunicazione dei dati, il CRC è invisibile: il famoso protocollo di comunicazione X.25 FCS (frame error detection sequence) è adottato da CRC-CCITT, WinRAR, Nero, ARJ, LHA e altri software di compressione. adottato È CRC32 e l'unità disco in lettura e scrittura utilizza CRC16, i formati universali di archiviazione delle immagini GIF, TIFF, ecc. Utilizzano anche CRC come mezzo di errore.
CRC La natura è il resto della divisione stampo-2, il divisore è diverso e il tipo di CRC è diverso. Tipicamente, il divisore del CRC è rappresentato da un polinomio generato.
Secondo l'ambiente e le abitudini dell'applicazione, CRC può essere suddiviso nei seguenti criteri:
1) cantiere CRC-12;
2) CRC- 16 iarde;
3) codice CRC-CCIT;
4) Codice CRC-32.
Il codice CRC-12 viene solitamente utilizzato per trasmettere stringhe a 6 bit.
Il codice CRC-16 e CRC-CCITT viene utilizzato per trasmettere stringhe a 8 bit, dove CRC-16 è adottato negli Stati Uniti, mentre CRC-CCITT è utilizzato nei paesi europei. Il codice CRC-32 è principalmente in una trasmissione sincrona chiamata Point-to-point.
2. Basic principium generandi in CRC codice
Qualsiasi codice costituito da una stringa binaria di bit può essere utilizzato solo del fattore '0' e '1'. Senso Unico. Ad esempio, il polinomio corrispondente al codice 1010111 è X6 + X4 + X2 + X + 1, e il polinomio è il codice 101111 corrispondente a X5 + X3 + X2 + X + 1.
Il polinomio standard del controllo di ridondanza del ciclo CRC comune è il seguente:
CRC (12 bit) = x ^ 12 + x ^ 11 + x ^ 3 + x ^ 2 + x + 1
CRC (16 bit) = x ^ 16 + x ^ 15 + x ^ 2 + 1
CRC (ccitt) = x^ 16 + x^ 12 + x^ 5 +1 .
CRC (32-bit) = x^ 32 + x^ 26 + x^ 23 + x^ 22 + x^ 16 + x^ 12 + x^ 11 + x^ 10 + x^ 8 + X^ 7 + x^ 5 + x ^ 4 + x ^ 2 + x + 1
Accipe in exemplum polynomiale CRC (16-bit) et eius cohibita parvus binarius respondens est 1 1000 0000 00000101.
Coefficientes utriusque polynomiae binarii sunt, et quattuor operationes implicatae adhuc sequuntur regulas calculi secundi formae.
(Nota: Quatuor operationes referuntur ad exemplum duarum bitarum inter binarios numeros, quos in calculi involvit, XOR diversus est vel computatus, nempe: 1 xor 1 = 0, 0 XOR 0 = 0, 1 xor 0 = 1 , 0 xor 1 = 1 , id est , idem est 0 , diversum est 1)
3. principium
si pone Codeword longitudo est n, notitia campi est k frenum, perscriptio campus est R frenum (n = k + r), tunc pro codice CRC, quaelibet vox codicis, existit et una tantum R temporibus polynomiae G (x) facit V (x) = a (x) g (x) = XRM (x) + R (x); in quibus: m (x) est k temporis notitia polynomialis, R (X) est R-1 polynomialis perscriptio, g (X) vocatur polynomialis generans: g (x) = g0 + g1x + g2x2 + ... + g (r. -1) x (r-1) + GRXR mittente verba generare CRC codicem G (X) ex G (x) recipere Fundatum in G (x) ad comprobandum receptam CRC codeword.
4. CRC represserat codice software generationis modum
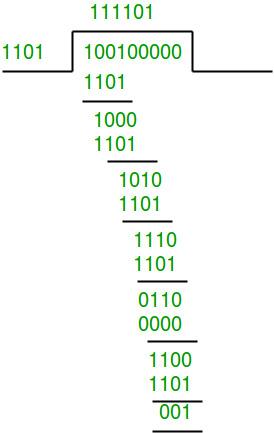
Reliquus numerus campus per divisionem polynomiam est perscriptio. Exempli gratia: Information ager code est: 1011001; Corresponde M (x) = x6 + x4 + x3 + 1 hypothesis polynomiae generatae: g (x) = x4+x3+1;, congruens g (x) codem est: 11001x4m(x) = X10+x8+x7+x4 Corresponding code is: 10110001000; Adjustabilis divisio: Numerus densitatis est: 1010 (i. e. ager calibrationis est: 1010) Pars mitte: Transmissus ager transmissus est: 10110011010 Notitia campi verificationis Receptoris campi: Eadem generationis codice utere ad reprimendam: Agrum receptum / codicem generationis ( Divisio binaria) Si amoveri potest, recte dat calculi gradus residuum (1010): divisio sine mathematicis significationibus, et est exemplar computatorii, id est, divisoris et divisoris, sunt diversae vel calculi. 10110010000/11001 = 1111101111011100 = 1010
5. Features
Si selectio polynomialis generata recte seligitur, CRC una methodo reprehendo efficax error est. In doctrina, error detectionis capacitatis cycli superuacanea cohibitandi probari potest quod sequentia lineamenta:
1) Omnes errores impares deprehendi possunt;
2) Error duplici frena omnia deprehendere potest;
3) Errorem continuum deprehendere potes qui longitudini calibrationis bis minus quam vel aequalis est;
4) continuum errorem maiorem quam longitudinem represserat cum probabilitate detegit.
