Tehoelektroniikkatekniikan kehityksen myötä erilaisia epälineaarisia kuormia on käytetty laajalti teollisuuden ja maatalouden tuotannossa ja siirtolaitteissa, mikä tekee sähköverkon aaltomuodon vääristymisestä, eli harmonisista häiriöistä, yhä vakavampia. Sähköverkon aaltomuodon vääristyminen aiheuttaa monia haittoja, kuten lisää moottorien, muuntajien, reaktorien jne. häviöitä, häiritsee tietoliikennelinjoja ja aiheuttaa koko sähköverkon osittaisen tai jopa halvaantumisen. Yliaaltojen paremmin vaimentamiseksi on välttämätöntä analysoida tarkasti sähköverkon harmoniset häiriöt. Jaksottaisten signaalien näytteistys- ja diskretisointiprosessissa käytetään yleensä kahta menetelmää. Yksi on kvasisynkroninen näytteistys, joka vaatii enemmän aaltomuotoja ja käyttää kvasisynkronisia algoritmeja useiden iteratiivisten operaatioiden suorittamiseen, mikä ei sovellu dynaamisten signaalien mittaamiseen; Toinen on synkroninen näytteenotto, joka on jaettu laitteiston synkroniseen näytteenottoon ja ohjelmistosynkroniseen näytteenottoon. Laitteiston synkroninen näytteenotto ottaa käyttöön vaihelukitun silmukkapiirin, joka on yleensä monimutkainen suunnittelultaan ja alhainen luotettavuus; ohjelmiston synkroninen näytteenotto ei vaadi lisälaitteistopiirejä, ja sen toteutustapa on joustava. Sitä on käytetty laajalti jaksollisten signaalien mittaamisessa. Koska AC-signaali on erityinen jaksollinen signaali, sen spektri on viivaspektri, joka on jakautunut perusaaltoon ja sen taajuuden kokonaislukukerrannaisiin. On tarpeen varmistaa, että näytteenottosignaali ja alkuperäinen signaali ovat tiukasti synkronoituja, eli näytteenottotaajuus on signaalitaajuuden kokonaislukukerrannainen, muuten se tulee Spektrivuodon esiintyminen aiheuttaa signaalin diskreetin Fourier-muunnoksen tuottaa testivirheitä ja vaikuttaa harmonisen analyysin tarkkuuteen. Sähköverkon taajuuden pienistä vaihteluista johtuen on väistämätöntä, että yllä oleva ilmiö tapahtuu, kun näytteenottotaajuus on kiinteä. Tästä syystä kotimaiset ja ulkomaiset tutkijat ovat ehdottaneet monia menetelmiä spektrivuotojen vaikutuksen vähentämiseksi mittaustarkkuuteen.
Spektrivuoto
Ns. spektrivuotolla tarkoitetaan signaalispektrin eri spektrilinjojen keskinäistä vaikutusta, jolloin mittaustulos poikkeaa todellisesta arvosta ja ilmaantuu samanaikaisesti muilla taajuuspisteillä spektriviivan molemmilla puolilla. väärät spektrit pienemmillä amplitudeilla. Yksinkertaisesti sanottuna spektrivuodon syy on se, että näytteenottotaajuutta ei ole synkronoitu signaalitaajuuden kanssa, jolloin jaksollisen näytteistyssignaalin vaihe on epäjatkuva alussa ja lopussa.
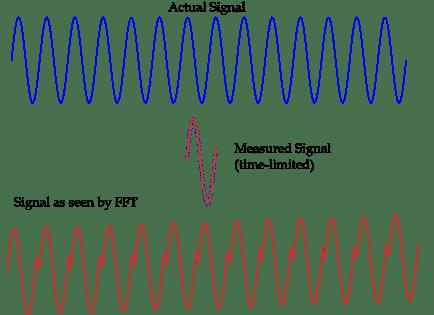
Ns. spektrivuoto on signaalispektrin eri spektrilinjojen keskinäinen vaikutus, joka saa mittaustuloksen poikkeamaan todellisesta arvosta. Väärä spektri. FFT:tä käyttämällä sähköjärjestelmän harmonisten analysointiin on mahdotonta välttää spektrivuodon ongelmaa. Tämä johtuu pääasiassa vaikuttavien tekijöiden luontaisesta epälineaarisuudesta, satunnaisuudesta, jakautumisesta, epästationaarisuudesta ja monimutkaisuudesta. Taajuus ei aina ole nimellistehotaajuuden vakioarvo, se muuttuu nimellistehotaajuuden ympärillä, joten ei voida taata, että reaaliaikainen taajuus on perustaajuuden kokonaislukukerrannainen, ja synkroninen näytteenotto ei voida saavuttaa. .
Kotimaassa ja ulkomailla ehdotetut menetelmät spektrivuotojen estämiseksi
Spektrivuodon suorin vaikutus on harmonisen analyysin epätarkkuus, joka puolestaan johtaa epätarkkoihin harmonisten analyysiin perustuvien sähköisten parametrien mittaamiseen. tarkka. Tietojen näytteenottopisteiden määrän lisääminen voi vähentää vuotoja, joiden ydin on suorakaiteen muotoisen ikkunan pääkeilan leveyden pienentäminen. Signaalin näytteenottotaajuuden lisääminen voi myös vähentää vuotoa. Tietojenkäsittelyn lisääntyneeseen määrään verrattuna edellä mainituilla kahdella menetelmällä on erittäin vähän parannusta vuotojen suhteen. Kirjallisuudessa ehdotetaan ikkunafunktioita ja interpolointitekniikoita. Ikkunatoiminnon valinnan perusperiaate on vaatia kapea pääkeila ja pieni sivukeila, jotta nämä kaksi vaatimusta voidaan ottaa mahdollisimman paljon huomioon, ja yleensä valitaan Hanning-ikkuna. Aikatasosta Hanning-ikkunan lisääminen tekee itse asiassa jaksollisen näytteenottosignaalin aloitus- ja loppupisteen vaiheeksi 0, mikä voittaa ilmiön, että näytteenottosignaalin vaihe on alussa ja lopussa epäjatkuva taajuusvaihteluiden vuoksi. , mutta mikä tahansa ikkunatoiminto on Ei pysty ratkaisemaan pääkeilan nollapisteen poikkeaman aiheuttamaa virhettä, joten vuotojen vähentäminen on myös rajoitettua. Interpolointitekniikka voi eliminoida vuotojen vaikutuksen lähes kokonaan, mutta tämän algoritmin tietojenkäsittelymäärä on liian suuri ja reaaliaikaista suorituskykyä on vaikea taata. Kirjallisuudessa ehdotetaan algoritmia spektrivuotojen vähentämiseksi. Sen ydin on, että kun näytteenottojakson ja näytteenottopisteiden lukumäärän tulo on yhtä suuri kuin signaalijakson kokonaislukukerrannainen, algoritmilla saatu diskreetti sekvenssi on signaalin näytteistyssekvenssi. Muussa tapauksessa algoritmi säätää näytteenottoa automaattisesti. järjestys. Simulaatio osoittaa, että algoritmi parantaa spektrivuotoa selvemmin, kun signaalin taajuuden vaihtelu ei ole suuri, ja algoritmin tarkkuus on pienempi, kun signaalitaajuuden vaihtelu on suuri. Yllä olevan algoritmin yleinen ominaisuus on korjata näytteenottosekvenssi tai taajuusspektri ratkaisematta spektrivuodon perimmäistä syytä. Tämä määrittää, että yllä oleva algoritmi tai vaikutus ei ole merkittävä tai että reaaliaikainen suorituskyky on huono. Spektrivuodon perimmäinen syy on fs≠Nf0. Spektrivuoto voidaan ratkaista tehokkaasti vain säätämällä fs reaaliajassa siten, että fs=Nf0. Yllä olevan tarkoituksen perusteella ehdotetaan algoritmia näytteenottotaajuuden adaptiiviseksi säätämiseksi, ja simulaatio todistaa algoritmin tehokkuuden.
Päätekijä, joka vaikuttaa tämän algoritmin nopeuteen, on FFT. Viime vuosina erityisesti tiedonkäsittelyyn sopivien DSP-sirujen ja niiden sovellusten jaksoittaisessa signaalianalyysissä ilmaantumisen myötä FFT-toiminnot ovat nopeutuneet jatkuvasti. VC5402:n käyttäminen 1024 pisteen monimutkaisten FFT-toimintojen suorittamiseen kestää vain 40 μs, mikä on täysin tyydyttävä. Järjestelmän reaaliaikaiset vaatimukset. Siksi tällä algoritmilla on vahva käytännön arvo järjestelmässä, joka perustuu AC-signaalin mittaukseen. Algoritmia sovelletaan parhaillaan vesivoimalaitosten valvontajärjestelmän suunnittelussa.
Spektrivuoto Fourier-muunnosprofilometriassa
Fourier-muunnosprofilometria (FTP) on yleisesti käytetty kolmiulotteinen pintamittausmenetelmä. Sen toimintaperiaate koostuu seuraavista kolmesta osasta: 1) Testattavan kolmiulotteisen kohteen pinnan muoto moduloi spatiaalisesti hilan rakenteellista valokenttää siten, että epämuodostunut rakenteellinen valokenttä kuljettaa tiedon kolmen ulottuvuuden korkeusjakaumasta. -ulotteinen pinnan muoto; 2) Jatkuvaa jakelua varten Epämuodostuneesta rakenteellisesta valokentästä otetaan näytteitä diskreetin tiedon saamiseksi helppoa tietokonekäsittelyä varten; 3) Tietokone suorittaa Fourier-muunnoksen saadulle diskreetille tiedolle, valitsee sopivan suodatinikkunan perustaajuuskomponentin suodattamiseksi spektristä ja kääntää perustaajuuskomponentin. Fourier-muunnos palauttaa mitatun pinnan korkeusjakauman.
Kun Fourier-muunnos suoritetaan diskreetille deformoituneelle rakenteelliselle valokentälle, diskreetti Fourier-muunnosalgoritmi edellyttää deformoituneen strukturoidun valokentän säännöllistä laajentamista avaruusalueella. Jakson pidentäminen voi aiheuttaa spektrivuotoja, joten Fourier-muunnosprofilometrian mittaukseen tulee virheitä, mutta harvat puhuvat siitä teoreettisesti. Jakson laajenemisen aiheuttaman spektrivuotojen vähentämiseksi ihmiset valitsevat usein sopivan ikkunatoiminnon (kuten Hanning-ikkunan) painottamaan epämuodostunutta valokenttää siten, että CCD:n näytteenottama epämuodostunut valokenttä käsitellään ikkunatoiminnolla ja ikkunan reunan intensiteetti on 0, ja sitten Fourier-muunnos. Kuitenkin sen jälkeen, kun ikkunatoiminto on käsitellyt signaalin, osa informaatiosta katoaa, mikä vastaa spektrivuodon vähentämistä ja aiheuttaa virheitä. Tässä artikkelissa analysoidaan epämuodostuneen valokentän spektrivuotojen ongelmaa rajoitetulla tilassa. Pidentyneen jakson ja deformoituneen rakenteen optisen kentän spektrivuodon välinen suhde johdetaan teoreettisesti ja esitetään virheen laskentamenetelmä ja kvantitatiivinen analyysi. On huomautettava, että vain kun laajennusjakso on yhtä suuri kuin hilajakson kokonaislukukerrannainen, laajentuneet reunat ovat jatkuvia, eikä Fourier-muunnos aiheuta spektrivuotoa; kun laajenemisjakso ei ole yhtä suuri kuin hilajakson kokonaislukukerrannainen, laajennetut reunat ovat epäjatkuvia. Varsinkin kun laajenemisjakson ja epämuodostuneen valokentän hilajakson kokonaislukukerrannan välillä on 0,5 hilajakson ero, reunamurtuminen on vakavin laajenemisen jälkeen ja spektrivuoto on suurin. Siksi, kun mittaat Fourier-muunnosprofilometrialla, yritä valita laajennusjakso, joka on yhtä suuri kuin signaalijakson kokonaislukukerrannainen spektrivuodon aiheuttaman mittausvirheen vähentämiseksi. Jos tämä ei ole mahdollista, voidaan käyttää iteratiivista menetelmää hapsujen ekstrapoloimiseksi uusien hapsujen luomiseksi tehokkaan näkökentän molemmille puolille vuotovirheen laajentamiseksi tehokkaan näkökentän ulkopuolelle ja reunavuotovirheen vähentämiseksi.
