Ongelman esittely
18. vuosisadalla Gobini, on joki läpi, on kaksi saarta, on Seitsemän siltaa yhdistää kaksi saarta joen rannalla (kuten ääriviivat kartta). Jotkut ovat ehdottaneet kysymystä: Miten jalankulkija ei toista, ei missaa seitsemää siltaa kerrallaan ja palaa lopulta lähtöpisteeseen. Myöhemmin suuri matemaatikko Euli muutti sen geometriseksi ongelmaksi - maalausongelmaksi. Hän ei vain ratkaissut tätä ongelmaa, vaan antaa myös täytön kuvan kaaviosta: Parittomien pisteiden määrä ei ole 0, on 2 (parillisten lukujen määrä, "jos se on Parillinen luku kutsutaan parilliseksi. Jos haluat piirtää kuvan, sinun on oltava parillinen keskellä, eli on toinen tapa saada toinen tapa, ja singulaarisuus voi olla vain molemmissa päissä, joten mikä tahansa figuuri voidaan piirtää, Oliko sinulla vai molemmat päät).
Päätelmämenetelmä
Kun Euler vieraili Preussin Gobisburgissa (nykyinen Venäjä Galoningrad), hän löysi erittäin mielenkiintoisen paikallisen yleisön. Konfutsea. Gobinic Cityssä on joki nimeltä Pregel, tämä mielenkiintoinen ajanviete on kävelymatkan päässä kaikista seitsemästä sillasta lauantaina, ja jokainen silta voi kulkea vain kerran ja lähtöpisteen on oltava sama. .
Euchi asettaa jokaisen palan pisteeseen, joka yhdistää kaksi maanpäällistä siltaa.
Sellaista on mahdotonta tiedustella. Hänen argumenttinsa on tämä, paitsi lähtökohta, joka kerta kun henkilö tulee maahan (tai pisteeseen) sillalla, hän (tai hän) myös poistuu tästä pisteestä toista siltaa pitkin. Siksi jokainen viiva on pisteessä, aloituspisteen ja viimeisen paluupisteen viivasta lasketaan kaksi siltaa (tai viivaa), joten muuhun maahan yhdistettyjen siltojen määrä on lähes parillinen.
On ongelma
Seitsemän siltaa, orientaatioiden lukumäärää ei sisällä pistettä, joten yllä olevia tehtäviä ei voida suorittaa.
Euler on erittäin tärkeä, se on myös erittäin älykäs, se osoittaa käytännön ongelmia käsittelevän matemaatikon ainutlaatuisuuden - abstraktii todellisen ongelman sopivaksi "matemaattiseksi malliksi". Tämä tutkimusmenetelmä on "Mathematical Model Method". Tämän ei tarvitse käyttää kuinka syvällistä teoriaa, mutta ajattele tätä, mutta avain ongelman ratkaisemiseen.
Seuraavaksi Euler käyttää kuvassa olevaa maalausta arvioidakseen suuntaviivoja ja arvioi nopeasti, että 7 siltaa eivät toista Doinsburgin satamaa kerran. Toisin sanoen, kuinka monta vuotta tulee, ihmiset kiinnittävät huomiota ei-toistuvaan reittiin, ei ole olemassa ollenkaan. Ongelma, jota on ollut vaikea elää, on itse asiassa niin vapaa vastaus!
Lopullinen saavutus
Ongelman alkuvaihe
Kun kysymys on esitetty, monet ihmiset ovat erittäin kiinnostuneita tästä, mutta he tekevät kokeiluja, mutta pitkään aikaan en ole koskaan ratkennut. Tavallisella matemaattisella tiedolla jokainen silta otetaan kerran, ja seitsemän siltaa kaikki kävelevät yhteensä 5040, ja niin monessa tapauksessa se on koe, joka tulee olemaan paljon työtaakkaa. Mutta kuinka voin löytää reitin, joka kulkee onnistuneesti jokaisen sillan läpi toistamisen sijaan? Siksi muodostuu kuuluisa "Gossoburgin seitsemän sillan ongelma".
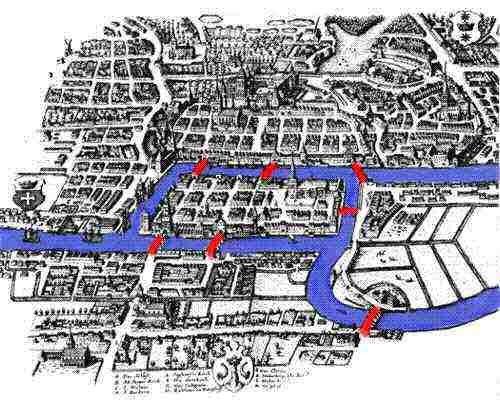
Ongelma Valottamisen jälkeen
1735, on useita korkeakouluopiskelijoita kirjoittaa kirje nerolle matemaatikko Euralle, joka työskentelee Venäjällä, Porsopian tiedeakatemiassa. Pyydä häntä auttamaan tämän ongelman ratkaisemisessa. Ou tarkkaili kovaa siltaa Gobissa ja ajatteli sitä vakavasti, mutta hän ei ollut onnistunut, joten hän epäili, ettei Qiqiaon kysymys ratkaissut sitä?
Vuonna 1736, vuoden tutkimuksen jälkeen, 29-vuotias Orap jätti "Gobi Seven Bridge" -paperit, ratkaisi onnistuneesti tämän ongelman ja loi uuden matematiikan haaran - Graph Theory.
Lehdessä Eutu tiivistää Qiqiao-kysymyksen ja ottaa jokaisen palan pisteeksi, yhdistää kaksi maasiltaa. Ja siten sai saman geometrian kuin kuvassa. Jos käytämme A, B, C, D neljää pistettä edustamaan Gobinicin neljää aluetta. Tällainen kuuluisa "seitsemän sillan ongelma" muunnetaan siihen, onko mahdollista käyttää ei-toistuvaa maalausta seitsemästä rivistä. Jos osaat piirtää, sinulla on oltava loppu- ja aloituspisteet grafiikassa, ja aloituspisteen ja loppupisteen tulee olla samat. Koska symmetria voidaan nähdä B:stä tai C:stä lähtöpisteenä, jos oletetaan, että A on aloituspiste ja päätepiste, niin On oltava yhden päässä johdosta ja vastaavasta sisääntulolinjasta. Jos määritämme A:een saapuvan linjan rivien lukumäärän, lankasta lähtevien rivien lukumäärä on ulostulo ja linjan sauvojen lukumäärä on A-aste, niin a Aste ja asteiden aste ovat yhtä suuret, eli A:n asteen tulee olla parillinen luku. Eli A:sta on tehtävä päättäjä. Epäkyvyttömyyden tulee olla parillinen luku, ja itse asiassa A:n aste on 5, on pariton, joten voidaan nähdä, että se on väistämätön A:sta. aika, jos se on B:stä tai D:stä, koska B:n, D:n asteet ovat 3, 3, jokainen on pariton, eli aloituskohta on julkaisematon.
Tiedetään, että edellä mainittu syy on se, että abstrakti matemaattinen ongelma on alilypistämätön, eli "seitsemän siltatehtävää" on myös julkaisematon.
From this we get: Euler loop relationship
Jotta voimme tietää, että A-grafiikka voidaan piirtää, sen on täytettävä seuraavat kaksi ehtoa:
1. Grafiikka on liitettävä.
2. "Todennäköisyyksien" lukumäärä kuvassa on 0 tai 2.
Voimme myös varmistaa, että grafiikka voidaan piirtää. Voidaan myös arvioida "seitsemän sillan ongelmaa", 4 pistettä on outoja, voi tietää, että kuvaa ei voi "piirtää", eli ei ole toistuvasti ohitettava kaikkia seitsemää siltaa.
Vuonna 1736 Eucula selitti ratkaisumenetelmänsä "Gobinburg 7 -sillan" papereissa, jotka luovutettiin Pietarin akatemialle. Hänen induktionsa loi perustan uudelle matemaattiselle haaralle - topologian perustamiselle.
Qiqiaon kysymys ja Eulerin lause
Euler omaksuu Qiqiao-kysymystä koskevan tutkimuksen, ei vain toistaakseen Gobinburgin asukkaiden ehdottamaa ongelmaa. Hän sai ja todisti kolme aivohalvaukseen liittyvää johtopäätöstä, ja ihmisiä kutsutaan usein Euler-lauseeksi. Yhdyskartassa sitä kutsutaan tavallisesti Euler Roadiksi solmusta piirretystä reitistä. Ihmiset kutsuvat yleensä paria Euler-piirejä, jotka vedetään takaisin lähtöpisteeseen. Euroopan silmukan sisältävää kuvaa kutsutaan Euler-kartaksi.
Tämä aihe sisältyy matematiikan matematiikan 12. kirjaan. 104 sivua.
Tämä aihe sisältyy myös ensimmäisen osan ensimmäiseen osaan. Sivulla 121.
Maalaus
⒈⒈⒈ ⒈ 通 通 通 图 图 图 图 图 图 图 图 图 图 图 通 图 图 图 图 图 图 图When you draw, you can take anything at the starting point, and finally you can draw this picture with this point.
⒉ Jos vain kaksi paritonta perspektiiviä (loppu on parillinen), se on piirrettävä. Kun piirrät, sinun on asetettava outo piste aloituspisteeksi ja toinen outo kohta on loppu.
⒊ Muita tilakarttoja ei voi piirtää. (Parittomien pisteiden määrä voidaan laskea toisessa kuvassa muutaman palan nostamiseksi.)
