taantumisanalyysi

Inbigdataanalysis,regressionanalysisisapredictivemodelingtechniquethatstudiestherelationshipbetweenthedependentvariable(target)andtheindependentvariable(predictor).Thistechniqueiscommonlyusedforpredictiveanalysis,timeseriesmodeling,anddiscoveryofcausalrelationshipsbetweenvariables.Forexample,thebestwaytostudytherelationshipbetweendriver'srecklessdrivingandthenumberofroadtrafficaccidentsisregression.

menetelmät

Therearevariousregressiontechniquesforprediction.Thesetechniquesmainlyhavethreemeasures(thenumberofindependentvariables,thetypeofdependentvariable,andtheshapeoftheregressionline).

1.Lineaarinen regressio

Itisoneofthemostwell-knownmodelingtechniques.Linearregressionisusuallyoneofthepreferredtechniqueswhenpeoplelearnpredictivemodels.Inthistechnique,thedependentvariableiscontinuous,theindependentvariablecanbecontinuousordiscrete,andthenatureoftheregressionlineislinear.

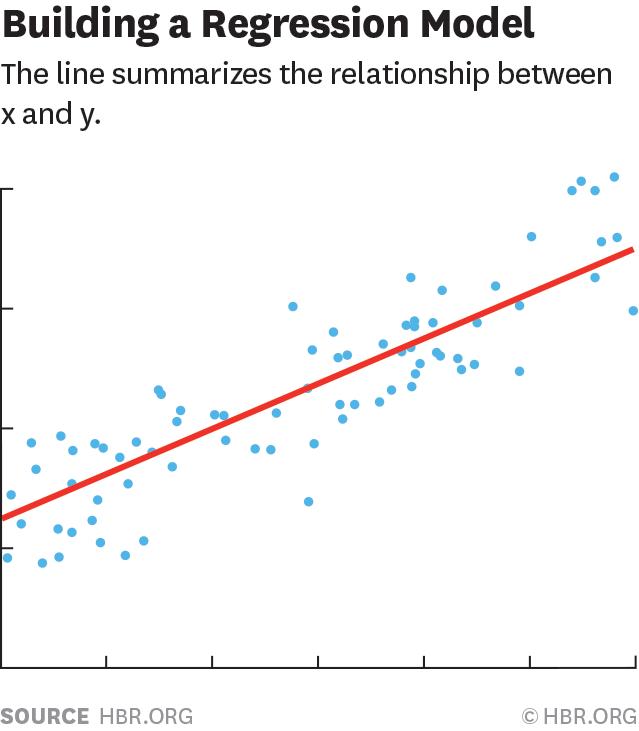
Linearregressionusesthebestfittedstraightline(alsoknownastheregressionline)toestablisharelationshipbetweenthedependentvariable(Y)andoneormoreindependentvariables(X).

Moniviivainen regressio voidaan ilmaista muodossa Y=a+b1*X+b2*X2+e,jossa edustaa leikkauspistettä, edustaa suoran kaltevuutta, ja on virhetermi. Moniviivainen regressio voi ennustaa kohdemuuttujan arvon annettujen ennustemuuttujien perusteella.

2.LogisticRegressionLogisticRegression

Logistista regressiota käytetään "tapahtuma=Onnistuminen"ja"tapahtuma=epäonnistumisen" todennäköisyyden laskemiseen. Kun riippuvaisen muuttujan tyyppi onbinaarinen(1/0,tosi/epätosi,kyllä/ei)muuttuja,logistiikkaregressioita tulisi käyttää.Tässä arvo on0 tai 1,jase voidaanilmaistalausekkeella.

kertoimet=p/(1-p)=tapahtuman todennäköisyys/huomautuksen tapahtuman todennäköisyys

ln(kertoimet)=ln(p/(1-p))

logit(p)=ln(p/(1-p))=b0+b1X1+b2X2+b3X3....+bkXk

Intheaboveformula,theexpressionphasTheprobabilityofacertainfeature.Youshouldaskthequestion:"Whyuselogarithmintheformula?".

Becausethebinomialdistribution(dependentvariable)isusedhere,itisnecessarytochoosealinkfunctionthatisbestforthisdistribution.ItistheLogitfunction.Intheaboveequation,theparametersareselectedbyobservingthemaximumlikelihoodestimatesofthesample,ratherthanminimizingthesumofsquareerror(asusedinordinaryregression).

3. Polynomiregressio

Foraregressionequation,iftheindeksioftheindependentvariableisgreaterthan1,thenitisapolynomialregressionequation.Asshowninthefollowingequation:

y=a+b*x^2

Inthisregressiontechnique,thebestfitlineisnotastraightline.Itisacurveusedtofitthedatapoints.

4.StepwiseRegression

Thisformofregressioncanbeusedwhendealingwithmultipleindependentvariables.Inthistechnique,theselectionofindependentvariablesisdoneinanautomaticprocess,includingnon-humanoperations.

Thisfeatistoidentifyimportantvariablesbyobservingstatisticalarvos,suchasR-square,t-statsandAICindicators.Stepwiseregressionfitsthemodelbyadding/removingcovariatesbasedonspecifiedcriteriaatthesametime.Someofthemostcommonlyusedstepwiseregressionmethodsarelistedbelow:

Thestandardstepwiseregressionmethoddoestwothings.Thatis,thepredictionrequiredforeachstepisaddedanddeleted.

Theforwardselectionmethodstartswiththemostsignificantpredictioninthemodel,andthenaddsvariablesforeachstep.

Thebackwardeliminationmethodstartsatthesametimeasallpredictionsofthemodel,andtheneliminatestheleastsignificantvariableateachstep.

Thepurposeofthismodelingtechniqueistousetheleastnumberofpredictorstomaximizepredictivepower.Thisisalsooneofthewaystodealwithhigh-dimensionaldatasets.2

5. RidgeRegression

Whenthereismultiplecollinearity(independentvariablesarehighlycorrelated)betweenthedata,ridgeregressionanalysisisrequired.Inthepresenceofmulticollinearity,althoughtheestimatedarvomeasuredbytheleastsquaremethod(OLS)doesnothaveabias,theirvariancewillbelarge,whichmakestheobservedarvoveryfarfromthetruearvo.Ridgeregressionreducesthestandarderrorbyaddingadeviationarvototheregressionestimate.

Inthelinearequation,thepredictionerrorcanbedividedinto2components,oneiscausedbybiasandtheotheriscausedbyvariance.Thepredictionerrormaybecausedbyeitherorbothofthese.Here,theerrorcausedbyvariancewillbediscussed.

Ridgeregressionsolvestheproblemofmulticollinearitythroughtheshrinkageparameterλ(lambda).Considerthefollowingequation:

L2=argmin||y=xβ||

+λ||β||

Inthisformula,Therearetwocomponents.Thefirstistheleastsquareterm,andtheotherisλtimesβ-square,whereβisthecorrelationcoefficientvector,whichisaddedtotheleastsquaretermtogetherwiththeshrinkageparametertogetaverylowvariance.

6. LassoRegressio

Itissimilartoridgeregression.Lasso(LeastAbsoluteShrinkageandSelectionOperator)willalsogiveapenaltyarvototheregressioncoefficientvector.Inaddition,itcanreducethedegreeofvariationandimprovetheaccuracyofthelinearregressionmodel.Takealookatthefollowingformula:

L1=agrmin||y-xβ||

+λ||β||

LassoregressionandRidgeregressionhaveOnedifferenceisthatthepenaltyfunctionitusesistheL1norm,nottheL2norm.Thisleadstoapenalty(orequaltothesumoftheabsolutearvooftheconstraintestimate)arvothatmakessomeparameterestimatesequaltozero.Thelargerthepenaltyarvois,thefurtherestimationwillmakethereductionarvoclosertozero.Thiswillresultintheselectionofvariablesfromthegivennvariables.

Ifthepredictedsetofvariablesishighlycorrelated,Lassowillselectoneofthevariablesandshrinktheotherstozero.

7. ElasticNetregression

ElasticNetisamixtureofLassoandRidgeregressiontechniques.ItusesL1fortrainingandL2firstastheregularizationmatrix.ElasticNetisusefulwhentherearemultiplerelatedfeatures.Lassowillpickoneofthematrandom,whileElasticNetwillchoosetwo.

ThepracticaladvantagebetweenLassoandRidgeisthatitallowsElasticNettoinheritsomeofthestabilityofRidgeintheloopstate.

Dataexplorationisaninevitablepartofbuildingapredictivemodel.Itshouldbethefirststepwhenchoosingasuitablemodel,suchasidentifyingtherelationshipandinfluenceofvariables.Moresuitablefortheadvantagesofdifferentmodels,youcananalyzedifferentindeksiparameters,suchasstatisticallysignificantparameters,R-square,AdjustedR-square,AIC,BIC,anderrorterms.TheotheristheMallows’Cpcriterion.Thisismainlybycomparingthemodelwithallpossiblesub-models(orchoosingthemcarefully)andcheckingforpossibledeviationsinyourmodel.

Crossvalidationisthebestwaytoevaluatepredictivemodels.Here,divideyourdatasetintotwo(onefortrainingandoneforvalidation).Useasimplemeansquareerrorbetweentheobservedarvoandthepredictedarvotomeasureyourpredictionaccuracy.

Ifyourdatasetismultiplemixedvariables,thenyoushouldnotchoosetheautomaticmodelselectionmethod,becauseyoushouldnotwanttoputallthevariablesinthesamemodelatthesametime.

Itwillalsodependonyourpurpose.Itmayhappenthatalesspowerfulmodeliseasiertoimplementthanahighlystatisticallysignificantmodel.Regressionregularizationmethods(Lasso,RidgeandElasticNet)workwellinthecaseofhigh-dimensionalandmulticollinearitybetweendatasetvariables.3

Oletukset ja sisältö

Indataanalysis,someconditionalassumptionsaregenerallyrequiredforthedata:

Varianssin homogeenisuus

Lineaarisuussuhteet

Vaikutusten kertyminen

Muuttujathavenomesurementerror

Muuttujat seuraavat monimuuttujanormaalijakaumaa

Tarkkaile itsenäisyyttä

Themodeliscomplete(novariablesthatshouldnotbeentered,andnovariablesthatshouldbeenteredarenotincluded)

Virhetermiriippumatonja noudattaa(0,1)normaalijakaumaa.

Realisticdataoftencannotfullycomplywiththeaboveassumptions.Therefore,statisticianshavedevelopedmanyregressionmodelstosolvetheconstraintsoftheassumedprocessoflinearregressionmodels.

Regressioanalyysin pääsisältö:

①Startingfromasetofdata,determinethequantitativerelationshipbetweencertainvariables,thatis,establishamathematicalmodelandestimatetheunknownparameters.Thecommonmethodofestimatingparametersistheleastsquaresmethod.

②Testaa näiden suhteiden uskottavuus.

③Intherelationshipwheremanyindependentvariablesaffectadependentvariabletogether,determinewhich(orwhich)independentvariableshavesignificanteffects,andwhichindependentvariableshaveinsignificanteffects,willaffectsignificantTheindependentvariablesareaddedtothemodel,andtheinsignificantvariablesareeliminated,usuallybystepwiseregression,forwardregression,andbackwardregression.

④Usetherequiredrelationshiptopredictorcontrolacertainproductionprocess.Theapplicationofregressionanalysisisveryextensive,andthestatisticalsoftwarepackagemakesthecalculationofvariousregressionmethodsveryconvenient.

Inregressionanalysis,variablesaredividedintotwocategories.Onetypeisdependentvariables,whichareusuallyatypeofindeksithatisconcernedinactualproblems,usuallyrepresentedbyY;andtheothertypeofvariablethataffectsthearvoofthedependentvariableiscalledindependentvariable,whichisrepresentedbyX.

Regressioanalyysitutkimuksen pääongelmat ovat:

(1)DeterminethequantitativerelationshipexpressionbetweenYandX,thisexpressioniscalledregressionequation;

(2)Testthereliabilityoftheobtainedregressionequation;

(3)DeterminewhethertheindependentvariableXhasaneffectonthedependentvariableY;

(4)Käytäsaadattua regressioyhtälöä ennustaaksesi ja ohjataksesi.4

Sovellus

Correlationanalysisstudiesthecorrelationbetweenphenomena,thedirectionandclosenessofcorrelation,andgenerallydoesnotdistinguishbetweenindependentvariablesordependentvariables.Regressionanalysisistoanalyzethespecificformsofcorrelationbetweenphenomena,determinethecausalrelationship,andusemathematicalmodelstoexpressthespecificrelationship.Forexample,itcanbeknownfromcorrelationanalysisthat"quality"and"usersatisfaction"variablesarecloselyrelated,butwhichvariablebetweenthesetwovariablesisaffectedbywhichvariable,andthedegreeofinfluence,requiresregressionanalysis.tomakesure.1

Generallyspeaking,regressionanalysisistodeterminethecausalrelationshipbetweendependentvariablesandindependentvariables,establisharegressionmodel,andsolvetheparametersofthemodelbasedonthemeasureddata,andthenevaluatetheregressionmodelWhetheritcanfitthemeasureddatawell;ifitcanfitwell,youcanmakefurtherpredictionsbasedontheindependentvariables.

Forexample,ifyouwanttostudythecausalrelationshipbetweenqualityandusersatisfaction,inapracticalsense,productqualitywillaffectusersatisfaction,sosetusersatisfactionasthedependentvariableandrecorditasY;Qualityistheindependentvariable,denotedasX.Thefollowinglinearrelationshipcanusuallybeestablished:Y=A+BX+§

where:AandBareundeterminedparameters,Aistheinterceptoftheregressionline;Bistheslopeoftheregressionline,whichmeansthatXchangesbyoneInunit,theaveragechangeofY;§isarandomerroritemthatdependsonusersatisfaction.

Empiiriselle regressioyhtälölle: y=0,857+0,836x

Theinterceptoftheregressionlineonthey-axisis0.857andtheslopeis0.836,whichmeansthatforeverypointinquality,usersatisfactionAnaverageincreaseof0.836points;inotherwords,thecontributionofa1pointimprovementinqualitytousersatisfactionis0.836points.

Theexampleshownaboveisasimplelinearregressionproblemofoneindependentvariable.Duringdataanalysis,thiscanalsobeextendedtomultipleregressionofmultipleindependentvariables.PleaserefertothespecificregressionprocessandmerkitysRefertorelevantstatisticsbooks.Inaddition,intheSPSSresultoutput,R2,FtestarvoandTtestarvocanalsobereported.R2isalsocalledthecoefficientofdeterminationoftheequation,whichindicatesthedegreeofinterpretationofthevariableXtoYintheequation.ThearvoofR2isbetween0and1.Thecloserto1,thestrongertheinterpretationabilityofXtoYintheequation.R2isusuallymultipliedby100%toexpressthepercentageofYchangeexplainedbytheregressionequation.TheFtestisoutputthroughtheanalysisofvariancetable,andthesignificancelevelisusedtotestwhetherthelinearrelationshipoftheregressionequationissignificant.Generallyspeaking,significancelevelsabove0.05aremerkitysful.WhentheFtestpasses,itmeansthatatleastoneoftheregressioncoefficientsintheequationissignificant,butnotallregressioncoefficientsaresignificant,soaTtestisneededtoverifythesignificanceoftheregressioncoefficients.Similarly,theTtestcanbedeterminedbythesignificanceleveloralook-uptable.Intheexampleshownabove,themerkitysofeachparameterisshowninthetablebelow.

Lineaariregressioyhtälön testi

SamplelinearregressionanalysisofSIMmobilephoneusersatisfactionandrelatedvariables

TakethelinearregressionanalysisofSIMmobilephoneusersatisfactionandrelatedvariablesasanexampletofurtherillustrateSovellusoflinearregression.Inapracticalsense,mobilephoneusersatisfactionshouldberelatedtoproductquality,price,andimage.Therefore,“usersatisfaction”isusedasthedependentvariable,and“quality”,“image”and“price”areindependentvariables.regressionanalysis.UsingtheregressionanalysisofSPSSsoftware,theregressionequationisobtainedasfollows:

Käyttäjätyytyväisyys = 0,008 × kuva + 0,645 × laatu + 0,221 × hinta

ForSIMmobilephones,thequalityisThecontributionofusersatisfactionisrelativelylarge.Forevery1pointincreaseinquality,usersatisfactionwillincreaseby0.645points;followedbyprice.Forevery1pointincreaseintheevaluationofpricesbyusers,theirsatisfactionwillincreaseby0.221points;andtheimageissatisfiedwiththeproductusers.Thecontributionofdegreeisrelativelysmall,andforevery1pointincreaseinimage,usersatisfactiononlyincreasesby0,008points.

Thetestindicatorsandtheirmerkityssoftheequationareasfollows:

Yhtälön testiindikaattorin kannalta "kuva" ei vaikuta paljoakaan koko regressioyhtälöön, ja se pitäisi poistaa. "Käyttäjien tyytyväisyys" ja "käyttäjien tyytyväisyys" pitäisi poistaa.

Everytimeauser’sevaluationofthepriceincreasesby1point,hissatisfactionwillincreaseby0.221points(inthisexampleIn,“image”hasalmostnocontributiontotheequation,sotheequationobtainedissimilartothecoefficientsofthepreviousregressionequation).

Thetestindicatorsandmerkityssoftheequationareasfollows:

Vaiheet muuttujien määrittämiseksi

Clarifythespecifictargetoftheprediction,andalsodeterminethedependentvariable.Ifthespecifictargetforforecastingisthesalesvolumeofthenextyear,thenthesalesvolumeYisthedependentvariable.Throughmarketresearchanddatareview,findtherelevantinfluencingfactorsoftheforecasttarget,thatis,independentvariables,andselectthemaininfluencingfactorsfromthem.

Ennakoivan mallin luominen

Calculatebasedonhistoricalstatisticaldataofindependentvariablesanddependentvariables,andestablishregressionanalysisequations,thatis,regressionanalysispredictivemodels.

Suorittaa korrelaatioanalyysiä

Regressionanalysisisthemathematicalstatisticalanalysisandprocessingofcausalinfluencingfactors(independentvariables)andpredictionobjects(dependentvariables).Onlywhentheindependentvariableandthedependentvariabledohaveacertainrelationship,theestablishedregressionequationismerkitysful.Therefore,whetherthefactorastheindependentvariableisrelatedtothepredictedobjectasthedependentvariable,thedegreeofcorrelation,andthedegreeofcertaintyinjudgingthedegreeofsuchcorrelation,havebecomeproblemsthatmustbesolvedinregressionanalysis.Forcorrelationanalysis,correlationisgenerallyrequired,andthedegreeofcorrelationbetweentheindependentvariableandthedependentvariableisjudgedbythesizeofthecorrelationcoefficient.

Laske ennustevirhe

Whethertheregressionpredictionmodelcanbeusedforactualpredictiondependsonthetestoftheregressionpredictionmodelandthecalculationofthepredictionerror.Onlywhentheregressionequationpassesvarioustestsandthepredictionerrorissmall,cantheregressionequationbeusedasapredictionmodelforprediction.

Determinethepredictedarvo

Usingtheregressionpredictionmodeltocalculatethepredictedarvo,andcomprehensivelyanalyzethepredictedarvotodeterminethefinalpredictedarvo.

Kiinnitä huomiota ongelmaan

Whenapplyingtheregressionpredictionmethod,firstdeterminewhetherthereisacorrelationbetweenthevariables.Ifthereisnocorrelationbetweenthevariables,applyingregressionforecastingmethodstothesevariableswillgivewrongresults.

Payattentiontothecorrectapplicationofregressionanalysisandprediction:

①Käytä laadullista analyysiä ilmiöiden välisen riippuvuuden määrittämiseksi;

②Vältä regressioennusteen ekstrapolointia;

③Soveltuvia tietoja;