Historiallinen tausta
Yli puoli vuosisataa ennen Maxwellin syntymää ihmiset ovat edistyneet suuresti sähkömagneettisten ilmiöiden ymmärtämisessä. Vuonna 1785 ranskalainen fyysikko C. A. Coulomb (Charles A. Coulomb) laati Coulombin lain, joka kuvaa kahden pistevarauksen välistä vuorovaikutusvoimaa vääntötasapainokokeen tulosten perusteella. Vuonna 1820 H. C. Oersted (Hans Christian Oersted) havaitsi, että sähkövirta voi kääntää magneettisia neuloja ja siten yhdistää sähkön magnetismiin. Myöhemmin A. M. Ampère (Andre Marie Ampère) tutki sähkövirtojen välistä vuorovaikutusta ja esitti monia tärkeitä käsitteitä ja Amperen silmukan lain. M. Faraday (Michael Faraday) on antanut huomattavan panoksen monissa asioissa, erityisesti vuonna 1831 julkaistussa sähkömagneettisen induktion laissa, joka on tärkeä teoreettinen perusta moottoreille, muuntajille ja muille laitteille.
Vuonna 1845 kolme tärkeintä sähkömagneettisia ilmiöitä koskevaa kokeellista lakia: Coulombin laki (1785), Biot-Savartin laki (1820), Faradayn sähkömagneettisen induktion laki (1831 - 1845) ) on tiivistetty Faradayn käsitteet "voimalinjasta" " ja "magneettinen voimalinja" (nykyisin myös "sähkökentän linja" ja "magneettinen voimalinja") on kehitetty "sähkömagneettisen kentän käsitteeksi". Vuodesta 1855 vuoteen 1865 Maxwell tarkasteli kattavasti Coulombin lakia, Biot-Savartin lakia ja Faradayn lakia ja toi matemaattiset analyysimenetelmät sähkömagneettisen tutkimuksen alalle, mikä johti Maxwellin sähkömagneettisen teorian syntymiseen. .
Ennen Maxwellia kaikki sähkömagneettisia ilmiöitä koskevat teoriat perustuivat ylietäisyyden toiminnan käsitteeseen. Uskottiin, että varattujen kappaleiden, magnetoitujen kappaleiden tai virtaa kuljettavien johtimien välinen vuorovaikutus voitaisiin suorittaa suoraan väliaineen ulkopuolella. Ja se tehdään välittömästi, eli sähkömagneettisen häiriön etenemisnopeutta pidetään äärettömänä. Tuolloin vain Faradaylla oli erilaisia mielipiteitä. Hän uskoo, että edellä mainitut vuorovaikutukset liittyvät välimediaan ja tapahtuvat välimedian siirron kautta eli puoltaen epäsuoran siirron teoriaa.
Maxwell peri Faradayn näkökulman, viittasi nestemekaniikan malliin, sovelsi tiukkoja matemaattisia muotoja tiivistämään edeltäjien työtä, ehdotti hypoteesin siirtymävirrasta, laajensi virran merkitystä ja päätteli sähkömagneettisen kentän peruslait. neljä differentiaaliyhtälöä, jotka ovat kuuluisia Maxwellin yhtälöitä. Hän analysoi tätä yhtälösarjaa ennakoiden sähkömagneettisten aaltojen olemassaolon ja päätteli, että sähkömagneettisten aaltojen etenemisnopeus on rajallinen arvo (lähellä valon nopeutta) ja että valo on myös tietyn taajuuden sähkömagneettinen aalto. Hän kirjoitti kaiken yllä olevan artikkelissaan "Sähköstä ja magnetismista".
Vuonna 1887 Heinrich R. Hertz käytti kokeellisia menetelmiä sähkömagneettisten aaltojen luomiseen ja havaitsemiseen, mikä vahvisti Maxwellin ennakoinnin. Vuosina 1905–1915 Albert Einsteinin suhteellisuusteoria osoitti edelleen ajan, tilan, massan, energian ja liikkeen välistä suhdetta, mikä osoittaa, että sähkömagneettiset kentät ovat aineen muoto ja epäsuora teoria on tunnustettu.
Yhtälön koostumus
Maxwellin yhtälöt koostuvat neljästä yhtälöstä:
Gaussin laki: Tämä laki kuvaa sähkökentän ja varauksen jakautumisen välistä suhdetta avaruudessa. Sähkökenttäviivat alkavat positiivisella varauksella ja päättyvät negatiiviseen varaukseen (tai äärettömään). Laske tietyn suljetun pinnan läpi kulkevien sähkökenttälinjojen lukumäärä, eli sen sähkövirta, ja saat selville tämän suljetun pinnan sisältämän kokonaisvarauksen. Yksityiskohtaisemmin tämä laki kuvaa mielivaltaisen suljetun pinnan läpi kulkevan sähkövirran ja suljetussa pinnassa olevan varauksen välistä suhdetta.
Gaussin magneettilaki: Tämä laki osoittaa, että magneettisia monopoleja ei todellisuudessa ole olemassa. Siksi ei ole eristettyä magneettista varausta, ja magneettikenttäviivalla ei ole alkupistettä eikä loppupistettä. Magneettikenttäviivat kiertävät tai ulottuvat äärettömyyteen. Toisin sanoen mille tahansa alueelle saapuvien magneettikenttälinjojen on poistuttava alueelta. Terminologiassa minkä tahansa suljetun pinnan läpi kulkeva magneettivuo on yhtä suuri kuin nolla tai magneettikenttä on passiivinen kenttä.
Faradayn induktiolaki: Tämä laki kuvaa kuinka ajassa muuttuva magneettikenttä indusoi sähkökentän. Sähkömagneettinen induktio on teoreettinen perusta monien generaattoreiden valmistukseen. Esimerkiksi pyörivä tankomagneetti synnyttää ajassa muuttuvan magneettikentän, joka puolestaan tuottaa sähkökentän, mikä saa viereisen suljetun piirin indusoimaan virtaa.
Maxwell-Amperen laki: Tämä laki sanoo, että magneettikenttä voidaan luoda kahdella tavalla: toinen on johtamalla virtaa (alkuperäinen Amperen laki) ja toinen ajassa muuttuvalla sähkökentällä tai siirtymävirralla (Maxwellin korjaustermi). .
Sähkömagnetiikassa Maxwellin korjaustermi tarkoittaa, että ajassa muuttuva sähkökenttä voi luoda magneettikentän, ja Faradayn induktiolain vuoksi ajassa muuttuva magneettikenttä voi tuottaa sähkökentän. Tällä tavalla nämä kaksi yhtälöä mahdollistavat teoriassa itseään ylläpitävien sähkömagneettisten aaltojen leviämisen avaruudessa.
Maxwellin sähkömagneettisen kentän teorian pääkohdat voidaan tiivistää seuraavasti:
①Useita erillisiä varautuneita esineitä tai virtoja, kaikki niiden välinen sähköinen ja magneettinen vuorovaikutus kulkee niiden välillä Mitä välittyy keskialueella, riippumatta siitä onko keskialue tyhjiö vai fyysinen aine.
②Sähköenergiaa tai magneettista energiaa ei ole vain varautuneissa kappaleissa, magnetoiduissa kappaleissa tai varautuneissa esineissä, vaan suurin osa siitä on jakautunut ympäröivään sähkömagneettiseen kenttään.
③Jos johtimen muodostamassa piirissä on katkos, piirissä oleva johtovirta kompensoituu eristeen siirtymävirralla, eli täysi virta on jatkuvaa. Ja siirtovirran ja sen synnyttämän magneettikentän välinen suhde on sama kuin johtavuusvirran suhde.
④ Magneettivuolla ei ole alkua eikä loppua, eli siinä ei ole magneettista varausta.
⑤Valoaallot ovat myös sähkömagneettisia aaltoja.
Maxwellin yhtälöt voidaan ilmaista kahdella tavalla.
1. Maxwellin yhtälöiden integraalimuoto on matemaattinen malli, joka kuvaa sähkömagneettista kenttää tietyllä tilavuudella tai alueella. Ilmaus on:
Equation ① is the law of total current derived from the generalization of the law of Ampere’s loop, and its meaning is: the line integral of the magnetic field intensity H along any closed curve is equal to the area passing through the limited area of this curve Full current. The first term on the right side of the equal sign is the conduction current. The second term is the displacement current. Equation ② is the expression of Faraday's law of electromagnetic induction, which shows that the line integral of the electric field intensity E along any closed curve is equal to the negative value of the rate of change of the magnetic flux passing through the area defined by the curve with respect to time. The closed curve mentioned here does not necessarily have to be composed of conductors, it can be a dielectric loop, or even just any closed contour. Equation ③ represents the principle of magnetic flux continuity, indicating that for any closed curved surface, as much magnetic flux enters the curved surface, the same amount of magnetic flux leaves. That is to say, the B line has neither a beginning nor a terminal; it also shows that there is no magnetic charge corresponding to the electric charge. Equation ④ is the expression of Gauss's law, which shows that under time-varying conditions, the net flux of D from any closed surface should be equal to the sum of all free charges in the volume enclosed by the closed surface.
2. Maxwellin yhtälöt differentiaalimuodossa. Maxwellin yhtälöiden differentiaalimuoto on jokaiselle kentän pisteelle. Del-operaattorilla ne voidaan kirjoittaa muodossa
Yhtälö ⑤ on kokonaisvirran lain differentiaalimuoto, joka osoittaa, että magneettikentän voimakkuuden H kiertymä on yhtä suuri kuin kokonaisvirrantiheys tässä pisteessä (johtamisvirran tiheys J ja siirtymävirran tiheys The summa), eli magneettikentän pyörrelähde on täysi virrantiheys, ja siirtymävirta voi luoda magneettikentän aivan kuten johtumisvirta. Kaava ⑥ on Faradayn sähkömagneettisen induktion lain differentiaalinen muoto, joka osoittaa, että sähkökentän voimakkuuden E kiertymä on yhtä suuri kuin magneettivuon tiheyden B aikamuutosnopeuden negatiivinen arvo tässä pisteessä, eli Sähkökentän pyörrelähde on magneettivuon tiheyden muutoksen aikanopeus. Yhtälö ⑦ on magneettivuon jatkuvuuden periaatteen differentiaalimuoto, joka osoittaa, että magneettivuon tiheyden B hajonta on aina nolla, eli B-linjalla ei ole alkua eikä loppua. Toisin sanoen ei ole sähkövarausta vastaavaa magneettista varausta. Yhtälö ⑧ on yleistys Gaussin sähköstaattisen kentän laista, toisin sanoen ajallisesti vaihtelevissa olosuhteissa sähkösiirtymän D divergentti on tässä vaiheessa edelleen yhtä suuri kuin vapaan varauksen tiheys.
Yllä olevien neljän yhtälön lisäksi vaaditaan välineen konstitutiivinen suhde
vihdoin ratkaista kenttämäärän ratkaisemisen ongelma. Missä ε on väliaineen dielektrisyysvakio, μ on väliaineen läpäisevyys ja σ on väliaineen johtavuus.
Ilmaisumuoto
Integroitu muoto
Maxwellin yhtälöiden integraalimuoto on seuraava:
Tämä on 1873 Noin vuoden aikana Maxwell ehdotti neljä yhtälöä, jotka ilmaisevat sähkömagneettisten kenttien yleistä lakia. Heidän joukossa:
(1) kuvaa sähkökentän luonnetta. Yleensä sähkökenttä voi olla vapaan varauksen sähkökenttä tai muuttuvan magneettikentän virittynyt indusoitu sähkökenttä, ja indusoitu sähkökenttä on pyörrekenttä, ja sen sähköinen siirtymälinja on suljettu eikä vaikuta vuotoon suljetusta kaarevasta pinnasta.
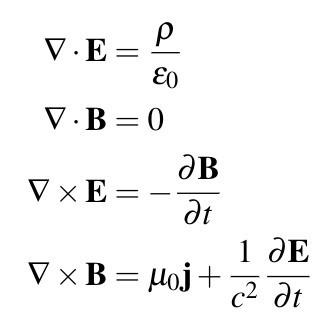
(2) kuvaa magneettikentän luonnetta. Magneettikenttä voidaan virittää muuttuvan sähkökentän johtavuusvirralla tai siirtymävirralla. Niiden magneettikentät ovat kaikki pyörrekenttiä, ja magneettiset induktiolinjat ovat suljettuja linjoja, jotka eivät vaikuta suljetun kaarevan pinnan virtaukseen.
(3) kuvaa muuttuvan magneettikentän lakia sähkökentän virittämiseksi.
(4) kuvaa virran johtavan lain ja sähkökentän muuttamisen magneettikentän virittämiseksi.
Lomake tasaiseen kenttään
Kun
, yhtälöt pelkistetään sähköstaattisen kentän ja tasaisen magneettikentän yhtälöiksi:
Lomake vapaassa tilassa ilman kenttälähdettä
Kun, the equation system becomes the following form:
The integral form of Maxwell's equations reflects the relationship between the amount of electromagnetic field (D, E, B, H) and the field source (charge q, current I) in a certain area of space.
Differentiaalinen muoto
Varsinaisessa sähkömagneettisen kentän käytössä on usein tarpeen tietää sähkömagneettisen kentän määrän piste pisteeltä avaruudessa sekä varauksen ja virran välinen suhde. Matemaattisesta muodosta Maxwellin yhtälöiden integraalimuoto muunnetaan differentiaalimuotoon. Käänteinen kolmio on Hamiltonin.
Huomautus:
(1) Eri inertiaviittauksilla Maxwellin yhtälöillä on sama muoto.
(2) Maxwellin yhtälöiden soveltamiseksi käytännön ongelmien ratkaisemiseen on myös otettava huomioon väliaineen vaikutus sähkömagneettiseen kenttään. Esimerkiksi yhtenäisessä ja isotrooppisessa väliaineessa sähkömagneettisen kentän määrällä on seuraava suhde väliaineen ominaisuuksiin:
Epäyhtenäisessä väliaineessa rajapinnan sähkömagneettisen kentän määrän raja-arvoa tulisi myös ottaa huomioon suhde. Käyttämällä kenttäsuureen alkuarvoehtoa, kun t=0, voidaan periaatteessa saada sähkömagneettinen kenttä missä tahansa avaruuden pisteessä milloin tahansa, nimittäin E(x, y, z, t) ja B(x, y, z, t).
Seuraavassa on Maxwellin yhtälöt Gaussin yksikköjärjestelmän alla
Fysikaalisten ominaisuuksien yhtälöt
Kun there is a medium, due to electric and magnetic fields The interaction with the medium makes the amount of electromagnetic field related to the characteristics of the medium. Therefore, the above-mentioned Maxwell equations are not complete at this time, and the physical property equations describing the properties of the medium (isotropic medium) need to be supplemented, respectively
Kaavassa ε, μ ja σ ovat johtimen absoluuttinen dielektrisyysvakio, absoluuttinen läpäisevyys ja johtavuus, vastaavasti Rate.
Teoreettinen lisätodistus siitä, että Maxwellin yhtälöt ja fysikaalisten ominaisuuksien yhtälöt yhdessä ovat täydellinen yhtälösarja sähkömagneettisen kentän muutosten määrittämiseksi. Toisin sanoen kun varaus ja virta on annettu, sähkömagneettisen kentän muutos voidaan määrittää täysin yllä olevasta yhtälöstä alkuehtojen (ja välttämättömien rajaehtojen) mukaan. Tietenkin, jos haluat keskustella sähkömagneettisen kentän vaikutuksesta varautuneisiin hiukkasiin ja varautuneiden hiukkasten liikkeisiin sähkömagneettisessa kentässä, tarvitset myös Lorentzin voimakaavan.
Monimutkainen numeromuoto
Sinimuotoisissa ajassa vaihtelevissa kentissä kompleksivektoreita voidaan käyttää sähkömagneettisten kenttien lain ilmaisemiseen kompleksilukuina.
Kompleksisessa sähkömagneettisen kentän laissa, koska kompleksikenttäsuure ja lähdesuure ovat vain avaruusaseman funktioita, ei ratkottaessa tarvitse ottaa huomioon niiden riippuvuutta ajasta. Siksi on kätevämpää käyttää sähkömagneettisen kentän monimutkaista lakia keskustelemaan sinimuotoisesta ajallisesti muuttuvasta kentästä.
Huomautukset
Käyttämällä eri yksikköjärjestelmiä Maxwellin yhtälöiden muotoa muutetaan hieman, ja yleinen muoto on edelleen sama, mutta eri vakiot ilmestyvät eri kohdille yhtälön sisällä.
Kansainvälinen yksikköjärjestelmä on yleisimmin käytetty yksikköjärjestelmä. Koko tekniikan ala käyttää tätä yksikköjärjestelmää. Useimmat kemistit käyttävät myös tätä yksikköjärjestelmää. Lähes kaikki korkeakoulun fysiikan oppikirjat käyttävät tätä yksikköjärjestelmää. Järjestelmä. Muita yleisesti käytettyjä yksikköjärjestelmiä ovat Gauss, Lorentz-Heaviside ja Planck. Senttimetri-gramma-sekunti-järjestelmästä johdettu Gauss-yksikköjärjestelmä soveltuu paremmin opetustarkoituksiin ja voi tehdä yhtälöistä yksinkertaisempia ja helpompia ymmärtää. Lorentz-Heaviside-yksikköjärjestelmä on myös johdettu senttimetri-gramma-sekunti-järjestelmästä ja sitä käytetään pääasiassa hiukkasfysiikassa; Planckin yksikköjärjestelmä on luonnollinen yksikköjärjestelmä, jonka yksiköt määritellään luonnon luonteen mukaan. Miehen asettama. Planckin yksikköjärjestelmä on erittäin hyödyllinen työkalu teoreettisen fysiikan opiskeluun ja se voi antaa suuren valaistuksen. Tällä sivulla, ellei toisin mainita, kaikki yhtälöt ovat kansainvälisessä yksikköjärjestelmässä.
Tässä esitetään kaksi Maxwellin yhtälöiden ekvivalenttia lauseketta. Ensimmäinen lauseke on seuraava:
Tämä lauseke lisää vapaan varauksen ja sidotun varauksen Gaussin lain vaatimaan kokonaisvaraukseen sekä jakaa vapaan virran, sidotun virran ja polarisaatiovirran. Kokonaismäärä on Maxwell-Amperen lain kokonaisvirta. Tämä ilmaus omaksuu suhteellisen perus- ja mikronäkökulman. Tätä lauseketta voidaan soveltaa laskemaan äärellisen lähdevarauksen ja lähdevirran tyhjiössä synnyttämät sähkö- ja magneettikentät. Todellisuudessa aineessa on kuitenkin liian paljon elektroneja ja atomiytimiä, joita ei voida ottaa mukaan laskelmaan. Itse asiassa klassinen sähkömagnetismi ei tarvitse niin tarkkoja vastauksia.
Toisen ilmaisun osalta katso "yleinen muoto" edellä mainitussa "integraatiolomakkeessa". Se ottaa lähteeksi vapaan varauksen ja vapaan virran, eikä se suoraan laske dielektrisessä aineessa esiintyvän sidotun varauksen ja magnetoidussa aineessa esiintyvän sidotun virran ja polarisaatiovirran osuutta. Koska yleisissä todellisissa olosuhteissa suoraan ohjattavia parametreja ovat vapaa varaus ja vapaa virta, ja sidottu varaus, sidottu virta ja polarisaatiovirta ovat ilmiöitä, jotka tapahtuvat aineen polarisoitumisen jälkeen. Tämän lausekkeen käyttö tekee dielektrisyydestä tai magnetoinnista. Erilaiset fysikaaliset laskelmat aineen sisällä ovat helpompia.
Pinnalla katsottuna Maxwellin yhtälöt näyttävät olevan ylimäärättyjä. Siinä on vain kuusi tuntematonta (vektorisähkökentässä ja magneettikentässä kummassakin kolme tuntematonta, virta ja varaus eivät ole tuntemattomia. Se on fysikaalinen suure, joka on vapaasti asetettu ja noudattaa varauksen säilymistä), mutta yhtälöitä on kahdeksan (kaksi Gaussia). laeilla on kaksi yhtälöä, Faradayn laki ja Amperen laki ovat vektoriaalisia, joista kukin sisältää kolme yhtälöä). Tämä tilanne liittyy Maxwellin yhtälöiden rajoitettuun toistettavuuteen. Teoriasta voidaan päätellä, että minkä tahansa järjestelmän, joka täyttää Faradayn lain ja Amperen lain, on täytettävä kaksi Gaussin lakia.
Toisaalta Maxwellin yhtälöt eivät ole suljettuja. Vain sähkömagneettisen väliaineen ominaisuudet huomioon ottaen tämä yhtälöjärjestelmä voi saada varman ratkaisun.
Sovellettava mittakaava
The Maxwell equations are usually applied to the "macro average field" of various fields. Kun the scale shrinks to the microscopic scale, so as to approach the size of a single atom, the local fluctuations of these fields will become unignorable, and quantum phenomena will begin to appear. Only under the premise of macro-average, some physical quantities such as the permittivity and permeability of a substance can get meaningful definition values.
Raskaimman ytimen säde on noin 7 femtometriä (1fm=10-15m). Siksi klassisessa sähkömagnetiikassa mikroskooppinen asteikko viittaa suuruusluokkaan, joka on suurempi kuin 10-14 m. Mikroskooppisen mittakaavan saavuttamiseksi elektroneja ja ytimiä voidaan pitää pistevarauksina, ja mikroskooppiset Maxwell-yhtälöt muodostetaan; Muuten ytimen sisäinen varausjakauma on otettava huomioon. Mikroskooppisella mittakaavalla laskettu sähkökenttä ja magneettikenttä muuttuvat edelleen melko rajusti, tilamuutoksen etäisyys on alle 10-10m ja ajanmuutoksen jakso 10-17 ja 10-13 sekuntia. Siksi mikroskooppisista Maxwell-yhtälöistä on suoritettava klassinen keskiarvooperaatio tasaisen, jatkuvan ja hitaasti muuttuvan makroskooppisen sähkökentän ja makroskooppisen magneettikentän saamiseksi. Makroasteikon alin raja on 10-8 metriä. Tämä tarkoittaa, että sähkömagneettisten aaltojen heijastus- ja taittumiskäyttäytyminen voidaan kuvata makro-Maxwell-yhtälöillä. Kun tämä minimiraja otetaan sivun pituudeksi, kuutio, jonka tilavuus on 10-24 kuutiota, sisältää noin 106 ydintä ja elektronia. Niin monien ytimien ja elektronien fyysinen käyttäytyminen klassisen keskiarvon jälkeen riittää tasoittamaan kaikki voimakkaat heilahtelut. Luotettavien kirjallisuustietojen mukaan klassinen keskiarvoistus vaatii vain avaruudessa, ei ajassa, eikä sen tarvitse ottaa huomioon atomien kvanttivaikutuksia.
Merkitys
Maxwellin panos kenttäkonseptin luomiseen on myös suuri innovaatio tuolloin fysiikassa, koska juuri kenttäkonseptin ilmaantuminen sai monet fysiikan tutkijat pääsivät eroon Newtonin "superetäisyyskonseptin" kahleista. ja yleisesti hyväksytty ajatus, että sähkömagneettiset ja gravitaatiovaikutukset ovat molemmat "läheisyys".
Maxwellin yhtälöiden sijainti sähkömagnetiikassa ja klassisessa sähködynamiikassa on sama kuin Newtonin liikelakien asema Newtonin mekaniikassa. Maxwellin yhtälöihin keskittyvä sähkömagneettinen teoria on yksi klassisen fysiikan ylpeimpiä saavutuksia. Sen paljastama sähkömagneettisen vuorovaikutuksen täydellinen yhtenäisyys on vakiinnuttanut fyysikot uskon, että aineen eri vuorovaikutukset tulisi yhdistää korkeammalla tasolla. Tätä teoriaa sovelletaan laajalti tekniikan aloilla.
Tieteellinen merkitys
(1) Klassisen kenttäteorian perusti Maxwell 1800-luvun lopulla yhteenvedon perusteella kolmesta sähkömagneettisen kokeellisesta laista ja vertaamalla niitä mekaanisiin malleihin. Mutta Maxwellin pääsaavutus juuri mahdollisti hänet murtautumaan klassisen mekaniikan rajoituksista: fysiikassa hän otti perustutkimuksen kohteena "kentän" "voiman" sijaan ja otti käyttöön vektorin osittaisen differentiaalioperaation, joka eroaa klassinen matematiikka matematiikassa. Symboli. Nämä kaksi ovat perusta sähkömagneettisen aallon yhtälön löytämiselle. Toisin sanoen Maxwellin työ on itse asiassa murtautunut klassisen fysiikan ja matematiikan puitteiden läpi tuolloin, mutta silloisten historiallisten olosuhteiden vuoksi ihmiset voivat edelleen ymmärtää sähkömagneettisen kentän teoriaa vain Newtonin laskennan ja klassisen mekaniikan viitekehyksestä. .
Moderni matematiikka, matemaattinen analyysi Hilbert-avaruudessa ilmestyi vasta 1800-luvun ja 1900-luvun vaihteessa. Kvanttimekaniikan aineaaltojen käsite löydettiin myöhemmin, varsinkin modernin matematiikan ja kvanttifysiikan erottamatonta matemaattista logiikkaa ei ole vielä täysin ymmärretty ja hyväksytty. Maxwellin sähkömagneettisen kentän teorian perustamisesta tähän päivään asti ihmiset ovat aina käyttäneet klassista matematiikkaa euklidisessa avaruudessa perusmenetelmänä Maxwellin yhtälöiden ratkaisemiseen.
(2) Maxwellin yhtälöiden syntymisestä, muodosta, sisällöstä ja historiallisesta prosessista voimme nähdä: Ensinnäkin fyysinen esine kehittyy uudeksi aksioomalausekkeeksi syvemmällä tasolla. Koska ihmiskunta hallitsee, tieteellinen kehitys ei kehity vakiintuneiden lähtökohtien alla. Uuden kognitiivisen merkityksen omaavan aksioomajärjestelmän perustaminen on merkki tieteen teoreettisesta edistymisestä. Toiseksi, vaikka fyysinen esine ja sen ilmaisutapa ovat eri asioita, on mahdotonta tunnistaa tämän objektin "olemassaoloa" turvautumatta oikeaan ilmaisumenetelmään. Kolmanneksi rakentamamme teoria määrittää sen merkityksen tason, jolla teemme esineistämme fyysisiä tosiasioita. Juuri tämän hämmennyksen nykyaikainen huippufysiikka tuo meille.
(3) Maxwellin yhtälöt paljastavat symmetrian kauneuden sähkö- ja magneettikenttien keskinäisessä muutoksessa. Tämä kauneus ilmaistaan täysin nykyaikaisessa matemaattisessa muodossa. Kuitenkin toisaalta meidän on myönnettävä, että vain oikea matemaattinen muoto voi täysin osoittaa eheyden (sähkömagneettisen symmetrian), jota ei voida nähdä empiirisessä menetelmässä; toisaalta emme saa unohtaa, että tämän symmetrian kauneus on matemaattisessa muodossa. Sähkömagneettisen kentän yhtenäinen luonne heijastuu. Siksi meidän tulisi ymmärtää, että meidän pitäisi "löytää" tai "nähdä" tämä symmetria matemaattisissa lausekkeissa sen sijaan, että päättelemme tämän olemuksen suoraan fysikaalisista matemaattisista kaavoista.
