In1801,ItalianastronomerGiuseppePiazzidiscoveredthefirstasteroidCeres.After40daysoftracking,PiazzilostthepositionofCeresbecauseCeresmovedtothebackofthesun.ThenscientistsallovertheworldusedPiazzi'sobservationaldatatostartsearchingforCeres,butsearchingforCeresbasedontheresultsofmostpeople'scalculationshasnoresults.TheorbitofCerescalculatedbyGauss,whowasonly24yearsold,wasconfirmedbytheobservationsoftheAustrianastronomerHeinrichAlbers,allowingtheastronomicalcommunitytopredicttheprecisepositionofCeres.ThesamemethodalsoproducedmanyastronomicalresultssuchasHalley'sComet.ThemethodusedbyGaussistheleastsquaresmethod,whichwaspublishedinhisbook"OntheMovementofCelestialBodies"in1809.Infact,theFrenchscientistLegendreindependentlyinventedthe"leastsquaresmethod"in1806,butitwasunknownbecauseitwasunknowntotheworld.
In1829,Gaussprovidedproofthattheoptimizationeffectoftheleastsquaresmethodisstrongerthanothermethods.
Määritelmä
Theleastsquaremethod(alsoknownastheleastsquaremethod)isamathematicaloptimizationtechnique.Itfindsthebestfunctionmatchofthedatabyminimizingthesumofsquaresoftheerror.Theleastsquaresmethodcanbeusedtoeasilyobtainunknowndataandminimizethesumofsquarederrorsbetweentheobtaineddataandtheactualdata.
Theleastsquaremethodcanalsobeusedforcurvefitting,andsomeotheroptimizationproblemscanalsobeexpressedbytheleastsquaremethodbyminimizingenergyormaximizingentropy.
Perusidea
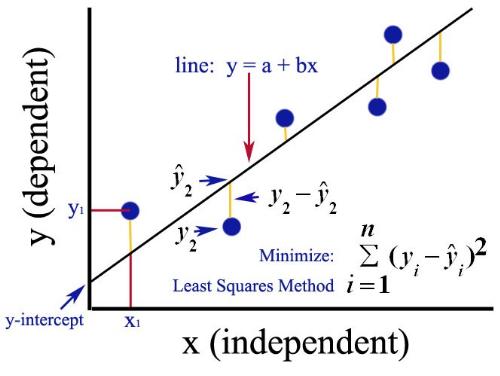
Theleastsquaremethodisthemostcommonlyusedmethodtosolvecurvefittingproblems.Thebasicideais:Let
Amongthem,isasetoflinearlyindependentfunctionsselectedinadvance,istheundeterminedcoefficient,andthefittingcriterionistominimizethesumofsquaresofthedistancebetweenand,Calledtheleastsquarescriterion.
Perusperiaate
Oletetaan, että (x,y) on havainnointipari ja täyttää seuraavat teoreettiset toiminnot:
jossa on määritettävä parametri.
Inordertofindtheoptimalestimatedvalueoftheparameterofthefunction,foragivengroup(usuallysection>)Observationdata,solvetheobjectivefunction
Taketheminimumparameter.Thistypeofproblemtobesolvediscalledaleastsquaresproblem,andthegeometriclanguageofthemethodtosolvethisproblemiscalledleastsquaresfitting.
Forunconstrainedoptimizationproblems,thegeneralformoftheleastsquaresmethodis:
whereCalledtheresidualfunction.Whenisalinearfunctionof,itiscalledalinearleastsquaresproblem,otherwiseitiscalledanonlinearleastsquaresproblem.
Pienimmän neliön optimointiongelma
Inunconstrainedoptimizationproblems,therearesomeimportantspecialcases,suchastheobjectivefunctionconsistingofthesumofthesquaresofseveralfunctions.ThistypeoffunctioncangenerallybeWrittenas:
Niistä yleensä vaatii ≥n. Minimoimme tämäntyyppisen toiminnon ongelman:
Itiscalledtheleastsquaresoptimizationproblem.Leastsquaresoptimizationisaspecialkindofoptimizationproblem.
Vähitenneliöestimaattorin ominaisuudet
Accordingtothesampledata,theleastsquaresestimatorcanbeusedtoobtaintheestimatorofthesimplelinearregressionmodelparameters.Buthowclosetheestimatorparameteristotheoveralltrueparameter?Whetherthereareotherbetterestimationformulas?Thisinvolvestheleastsquaresestimationformulaortheminimumvariance(orbest)(Best)oftheestimator,linearity(Linear)Andunbiased(Unbiased),referredtoasBLUcharacteristics.Thisisthemainreasonforthewidespreaduseofordinaryleastsquarestoestimateeconometricmodels.Thefollowingprovesthattheordinaryleastsquaresestimatorhastheabovethreecharacteristics.
1.Linearkaraktinen
Theso-calledlinearcharacteristicmeansthattheestimatoristhelinearfunctionofthesampleobservationvalue,thatis,thelinearcombinationoftheestimatorandtheobservationvalue.
2. Puolueettomuus
Unbiasednessmeansthattheexpectedvaluesofparameterestimatorsareequaltotheoveralltrueparameters.
3.Minimumvariance-ominaisuus
Theso-calledminimumvariancepropertyreferstotheminimumvarianceoftheestimatorcomparedwiththeestimatorobtainedbyothermethods,thatis,thebest.Theminimumvarianceisalsocalledeffectiveness.ThispropertyisthefamousGauss-Markov(Gauss-Markov)theorem.Thistheoremstatesthattheordinaryleastsquaresestimatoristhebestcomparedwithanylinearunbiasedestimatorobtainedbyothermethods.
