Taustatieto
TheID3-algoritmiwasfirstproposedbyJ.RossQuinlanattheUniversityofSydneyin1975asaclassificationpredictionalgorithm.Thecoreofthealgorithmis"informationentropy"..TheID3-algoritmicalculatestheinformationgainofeachattributeandconsidersthattheattributewithhighinformationgainisagoodattribute.Eachtimetheattributewiththehighestinformationgainisselectedasthepartitionstandard,thisprocessisrepeateduntiladecisiontreethatcanperfectlyclassifytrainingexamplesisgenerated.
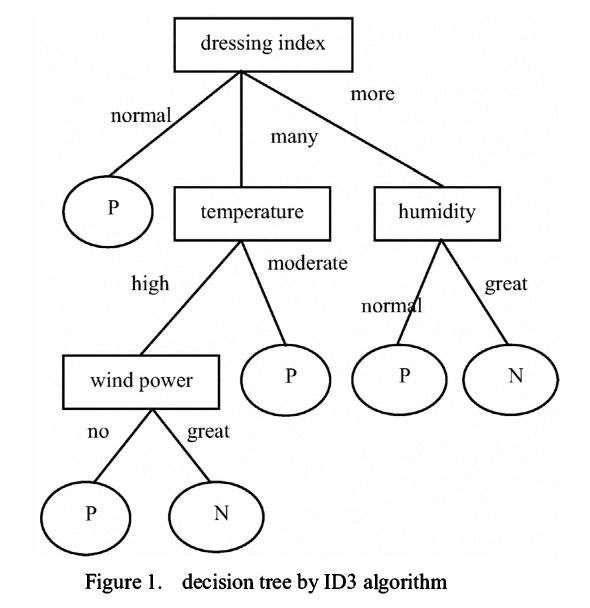
Decisiontreeistoclassifydatatoachievethepurposeofprediction.Thedecisiontreemethodfirstformsadecisiontreebasedonthetrainingsetdata.Ifthetreecannotgivethecorrectclassificationtoallobjects,selectsomeexceptionstoaddtothetrainingsetdata,andrepeattheprocessuntilthecorrectdecisionsetisformed.Thedecisiontreerepresentsthetreestructureofthedecisionset.
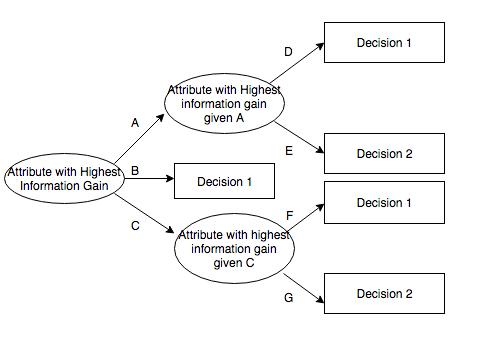
Thedecisiontreeiscomposedofdecisionnodes,branchesandleaves.Thetopnodeinthedecisiontreeistherootnode,andeachbranchisanewdecisionnode,oraleafofthetree.Eachdecisionnoderepresentsaproblemordecision,andusuallycorrespondstotheattributesoftheobjecttobeclassified.Eachleafnoderepresentsapossibleclassificationresult.Intheprocessoftraversingthedecisiontreefromtoptobottom,eachnodewillencounteratest,andthedifferenttestoutputsoftheproblemoneachnodewillleadtodifferentbranches,andfinallyaleafnodewillbereached.ThisprocessItistheprocessofusingdecisiontreestoclassify,usingseveralvariablestodeterminethecategoryitbelongsto.
ID3-algoritmi
TheID3-algoritmiwasfirstproposedbyQuinlan.Thealgorithmisbasedoninformationtheory,andusesinformationentropyandinformationgainasmeasurementstandards,soastorealizetheinductiveclassificationofdata.Thefollowingaresomebasicconceptsofinformationtheory:
Määritelmä1: Jos viestejä tulee samalla todennäköisyydellä, viestin todennäköisyys on 1/n ja viestin lähettämän tiedon määrä on-Log2(1/n)
Määritelmä2:Jos viestejä tulee jaantettu todennäköisyysjakauma onP=(p1,p2...pn),jakelun välittämän tiedon määrää kutsutaan P:n entropioksi.
.
Määritelmä3:JostietuejoukkoJaettu itsenäisiin luokkiinC1C2..kategorian määritteen arvon mukaan tarvittavien tietojen määrä määrittää, minkä luokan T:n elementti onInfo(T)=I(p),jossaPisthetodennäköisyysjakaumaC,/T|
Definition4:IfWefirstdivideTintosetsT1,T2...Tnaccordingtothevalueofthenon-categoryattributeX,andthendeterminetheamountofinformationofanelementclassinTcanbeobtainedbydeterminingtheweightedaveragevalueofTi,thatis,theweightedaveragevalueofInfo(Ti)is:
Info(X,T)=(i=1tonsum)((|Ti|/|T|)Info(Ti))
Definition5:InformationGainisthedifferencebetweentwoamountsofinformation.OneamountofinformationistheamountofinformationofoneelementofTthatneedstobedetermined,andtheotheramountofinformationistheamountofinformationofoneelementofTthatneedstobedeterminedafterthevalueofattributeXhasbeenobtained.Theinformationgaindegreeformulais:
Vahvistus(X,T)=Tiedot(T)-Info(X,T)
ID3-algoritmicalculatestheinformationgainofeachattribute,Andselecttheattributewiththehighestgainasthetestattributeofthegivenset.Createanodefortheselectedtestattribute,markitwiththeattributeofthenode,createabranchforeachvalueoftheattributeanddividethesampleaccordingly.
Tietojen kuvaus
Käytetyillä näytetiedoilla on tiettyjä vaatimuksia.ID3 on:
Description-attribute-attributeswiththesamevaluemustdescribeeachexampleandhaveafixednumberofvalues.
Ennalta määritetyt luokka-instanssiattribuutit täytyy olla määritettynä, eli niitä ei ole opittuID3.
Diskreettiluokka - luokan on oltava terävä ja erottuva. Jatkuvien luokkien jakaminen sumeisiin luokkiin (kuten metallit, jotka ovat "kovia, vaikeita, joustavia, lempeitä ja pehmeitä" ei ole uskottavaa.
Enoughexamples-becauseinductivegeneralizationisusedfor(Thatis,itisnotpossibletofindout.)Enoughtestcasesmustbeselectedtodistinguishvalidpatternsandeliminatetheinfluenceofspecialcoincidencefactors.
Attribuuttien valinta
ID3determineswhichattributesarebest.Astatisticalfeature,calledinformationgain,usesentropytoobtainagivenattributetomeasurethetrainingexamplesbroughtintothetargetclass.Theinformationwiththehighestinformationgain(informationisthemostusefulcategory)isselected.Inordertoclarifythegain,wefirstborrowfrominformationtheoryOnedefinitioniscalledentropy.Everyattributehasanentropy.
