Järjestelmän esittely
Kun tutkitaan kvantifioitua tarkkaa järjestelmää, joka ei osallistu, on olemassa joukko tehokkaita järjestelmäteorioita; mutta ihmisen konejärjestelmässä, johtamisjärjestelmässä, talousjärjestelmässä, yhteiskunnassa Sellaisissa järjestelmissä kuin ihmisen ajattelutoiminnassa järjestelmä ei ole täysin tarkka ihmisaivojen logiikan, päättelyn, harkinta- ja päätöksenteon vuoksi, tällä liittyvällä järjestelmällä on jonkinlainen sumeasta. Kun elektroninen digitaalinen tietokone kehittyy älykkään koneen suuntaan, tulee yhä enemmän sumeita järjestelmiä.
Tavanomaisessa järjestelmäteoriassa järjestelmä on selkeästi määrätty tietyllä aikatilalla ja -syötöllä, ja seuraavan hetken tila ja lähtö ovat selvästi ainutlaatuisia. Tätä järjestelmää kutsutaan deterministiseksi järjestelmäksi, muuten Sitä kutsutaan ei-deterministiseksi järjestelmäksi. Oletetaan, että järjestelmän tila ja syöttö tietyllä hetkellä, vaikka seuraavan kerran tilaa ja lähtöä ei voida määrittää, mutta se voi määrittää seuraavan tilan todennäköisyysjakauman, tätä järjestelmää kutsutaan satunnaiseksi järjestelmäksi, joka on päättämättömyyden luokka. Seksuaalinen järjestelmä. Jos seuraavan tilan todennäköisyysjakaumaa ei ole mahdollista määrittää, on mahdollista määrittää seuraavan kerran mahdollisen tilan kokoelma, joka on toisen tyyppinen epädeterministinen järjestelmä. Jos tämän ei-laadullisen järjestelmän mahdollisten tilojen joukkoa edustaa sumea kokoelma, sitä kutsutaan sumeaksi järjestelmäksi.
Sumea järjestelmä on sama kuin klassinen järjestelmä, sen tutkimussisältöön kuuluu myös energia, voi havaita, minimaalinen toteutus, järjestelmän tunnistaminen, ennustaminen, ohjaus ja vakaus.
Sumean logiikan perusta
Sumeaa settiä
Monien ihmisten ajattelulla ei ole selkeää laajennusta, kuten "iso", "keskikokoinen", "pieni" Odota, näitä sumeita käsitteitä ei voi kuvata klassisessa kokoelmassa. Professori Zadeh, professori Zadeh, ehdotti kuvailemaan näitä sumeita käsitteitä, jotka määritellään seuraavasti:
given the domain u, u to [0, 1] closed interval
is called a blurred subset of u,
Subjektiivisuustoiminto
Yleisiä jäsenfunktioita on useita tyyppejä: kolmiofunktiot (Kuva 1-1), tikapuufunktiot (Kuva 1-2), Gaussin tyyppiset funktiot (Kuva 2-1), Zhongmoid-funktiot (Kuva 2-2), Sigmoid-tyyppiset funktiot ( Kuva 3-1) ja Z-tyyppinen toiminto (Kuva 3-2).
Kolmiofunktio ja tikapuufunktio ovat pohjimmiltaan segmenttilineaarisia funktioita, joten niitä on suhteellisen helppo käyttää ja laskea.
Gaussin jäsenyysfunktio ja kellon jäsenfunktiokäyrä ovat hyvät sileät, ja grafiikka ei ole nolla ja niillä on suhteellisen selkeä fyysinen merkitys, joka on yleisimmin käytetty jäsenyysfunktio.
Sigmoid-tyypin jäsenyysfunktiokäyrällä on myös hyvä sileä, erilainen kuin Gaussin jäsenyysfunktio, ja SigmoID-tyyppinen jäsenyysfunktio sopii epäsymmetrisyyskeinoihin. Z-tyypin jäsenyysfunktio perustuu spline-interpolaatioon.
Perusarkkitehtuuri
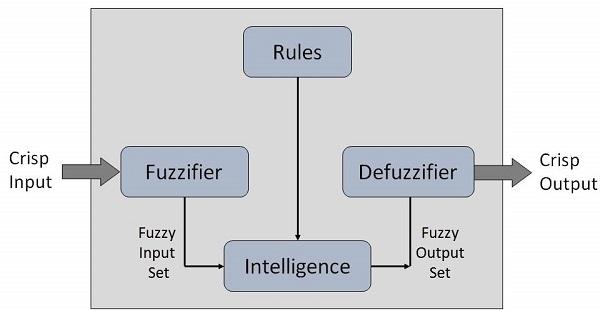
Sumea järjestelmä Perusarkkitehtuuri Kuten kuvassa 4 näkyy, päätoimintolohko sisältää: moniselitteisyysmekanismin, sumean sääntöpohjan, sumean päättelyn ja deprive-mekanismin.
Sumea mekanismi
Ambitating-mekanismin tehtävänä on muuntaa selkeä ulkoinen syöttödata sopivan kielen sumeaksi informaatioksi; toisin sanoen selkeät tiedot hämärtyvät sumennustiedoiksi.
Sumea sääntökirjasto
1, kielen sumeat säännöt (Mamdani sumeat säännöt):
then 2, toiminnalliset sumeat säännöt:
the
(1) lineaariset sumeat säännöt:
(2) yhden pisteen sumeat säännöt:
Then
(3) Tsukamoto Fuzzy Rule: Rear Part of this Fuzzy rule
Näillä sumeilla säännöillä perustellaan järkevästi päättelymoottoria, joka määrittää seuraavassa vaiheessa tehtävän päätöksen. Tärkeimmät erot edellä olevissa kolmessa säännössä ovat erilaisia vain sumeiden sääntöjen takana.
Sumea johtopäätös
Sumea päättelymoottori on sumean järjestelmän ydin, joka voi simuloida ihmisen ajattelun päätöstapoja likimääräisellä päättelyllä tai sumealla päättelyllä ongelmien ratkaisemiseksi Päivämäärä.
Defuusiomekanismi
kulkee sumean päättelyn ja numeerisen arvon selkeyttämisprosessin läpi, kutsumme "riistää".
Erilaisista sumeista säännöistä johtuen se on erilainen, vankila, sumean päättelyn jälkeen hypoteesi ilmaistaan sumeana kokoelmana (kuten kielen sumeussääntönä) ja Jotkut ilmaistaan selkeänä arvona.
Koska päättely on sumea joukko, yleisesti käytetyllä deprive-menetelmällä on painopiste, maksimikeskiarvomenetelmä, maksimikeskiarvomenetelmä, keskiarvomenetelmä ja korjauskeskus; päättelyn jälkeen on selvää. Jos arvo, painokeskiarvomenetelmä on yleisimmin käytetty deprive-menetelmä.
ominaisuudet
Sumean järjestelmän etuna on, että se voidaan integroida asiantuntijakokemukseen ja yleistyskyky on datan varassa. Asiantuntijakokemuksen kielenkäytön ansiosta sumeaa päättelyjärjestelmää on sovellettu monilla tekniikan aloilla. Nykyinen sumean logiikan järjestelmän syöttö on kuitenkin täysin tarkka tai täydellinen sumeuskokoelma, joka on ehkä syötettävä samaan aikaan sovelluksessa. Tarkkoja arvoja ja sumeita kielimuuttujia on parannettava olemassa olevissa sumeissa järjestelmissä; input, output space jako ja jäsenyys toiminto ja sen parametrit ovat pääasiassa luottaa henkilökohtaiseen kokemukseen, usein tarvitaan toistuvaa oikeudenkäyntiä, Erittäin subjektiivinen ja epävarmuus.
Sumea järjestelmätyyppi
Pure Fuzzy Logic System
Pure Fuzzy Logic System koostuu vain sumeista säännöistä ja sumeista vahvistuskoneista. Kuten kuvasta 5 näkyy, sen syöttö ja lähtö on sumea joukko. Koska puhtaan sumean logiikkajärjestelmän syöttö ja lähtö on sumea kokoelma, useimpien todellisen maailman suunnittelujärjestelmien syöttö ja lähtö ovat tarkkoja, joten puhdasta sumeaa logiikkaa ei voida suoraan soveltaa varsinaiseen suunnitteluun. Tämän ongelman ratkaisemiseksi tutkijat ehdottivat Mamdanin sumeaa logiikkaa, jossa on sumea generaattori ja epätarkkuuden eliminointi, joka perustuu puhtaaseen sumeaan logiikkajärjestelmään, ja japanilainen tieteellinen korkea puu (sugeno) ehdotti sumeaa sääntöä. Jälkimmäinen johtopäätös on tarkan arvon sumea järjestelmä, jota kutsutaan korkealaatuiseksi - sulkevaksi sumeaksi logiikkajärjestelmäksi.
Gaogu - Guan Yeno type fuzzy logic system
Gao Wume - Guan Yeeno -tyyppinen sumean logiikkajärjestelmän rakenne Kuva 6 osoittaa, että se on luokka erikoisempia sumealogiikkajärjestelmiä, jotka eroavat yleisen sumean säännön muodossa. Gaowu-Guanye-tyyppisen sumean logiikkajärjestelmän tulos on edelleen tarkka arvo ilman epätarkkuuden poistamista. Sen etuna on, että lähtö voidaan ilmaista tuloarvojen lineaarisella yhdistelmällä, koska menetelmä voidaan tuoda parametrien estimointiin järjestelmän parametrien määrittämiseksi, ja se voidaan likimääräisesti analysoida ja suunnitella sumea logiikkajärjestelmä lineaarisella ohjauksella. järjestelmäanalyysimenetelmä. Järjestelmän haittana on, että säännön tulososalla ei ole sumean kielen arvoa, joten se ei hyödynnä asiantuntemusta, ja myös erilaiset sumean logiikan periaatteet ovat rajoitettuja tässä järjestelmässä.
Mamdani sumea järjestelmä
Mamdani-tyyppisessä sumeassa järjestelmässä sumeiden sääntöjen etu- ja takaosa ovat sumean kielen arvoja, mikä on oleellisesti Puhtaan sumean logiikkajärjestelmän tulo- ja lähtöosat lisäävät sumean generaattorin ja sumeuden eliminoinnin, ja rakenne on esitetty kuviossa 1. Järjestelmän tulo ja lähtö ovat tarkkoja, joten niitä voidaan soveltaa suoraan varsinaiseen suunnitteluun. Laajan käyttötarkoituksensa ansiosta se tunnetaan myös sumean järjestelmän vakiomallina.
