määritelmä
on funktio, joka määrittelee toimialueet ja arvoalueet ovat reaalilukuja, jos argumentti on olemassa, tee siitä nimeltä epäjatkuvat funktiot . Toisin sanoen funktion arvo poikkeaa kiinteää pistettä vastaavasta arvosta missä tahansa kohdassa, jossa kiinteä piste on lähempänä. Esimerkiksi Diidge-funktio ei ole jatkuva funktio kaikkialla.
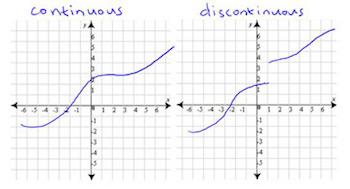
Epäjatkuvien funktioiden määritelmän mukaan se on yksinkertainen ja intuitiivinen tapa. Disconneitya käytetään myös monilla eri aloilla, kuten fysiikassa, lääketieteessä, taloustieteessä jne., myös käsitteet eri aloilla ovat erilaisia. Erityisesti fysiikan kvanttimekaniikka on tehnyt hyvän tulkinnan epäjatkuvuuksien luonteesta.
Esimerkki
Kvantti on tärkeä käsite nykyfysiikassa. Varhaisin on M. Prank, jota ehdotettiin vuonna 1900. Hän olettaa, että säteilyenergia mustassa kappaleessa on epäjatkuvaa ja voi ottaa vain energian perusyksikön kokonaislukukerran. Myöhemmin tutkimukset osoittavat, että energialla ei ole vain tätä epäjatkuvaa erotteluominaisuutta, vaan myös muissa fysikaalisissa suureissa, kuten kulmaliikemäärä, spin, varaus jne., on tämä epäjatkuva kvantisointi. Tämä on perustavanlaatuinen ero Newtonia-mekaniikan edustaman klassisen fysiikan välillä. Kvantisiset ilmiöt ilmenevät pääasiassa mikroskooppisessa fysikaalisessa maailmassa. Mikroskooppista maailmaa kuvaava fysikaalinen teoria on kvanttimekaniikka.
