definition
is a function, defining the domains and value domains are real numbers, if there is an argument, existence, make it called discontinuous functions . In other words, the value of the function is deviated from the value corresponding to the fixed point at any point where the fixed point is closer. For example, the Diidge function is a no continuous function everywhere.
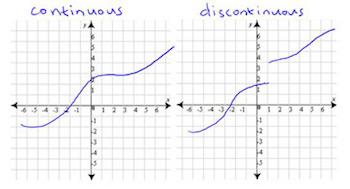
By the definition of discontinuous functions, it is a simple and intuitive way. Disconneity is also used in a wide variety of fields, such as physics, medicine, economics, etc., the concepts in different fields are also different. In particular, quantum mechanics in physics have done a good interpretation on the nature of discontinuities.
Example
Quantum is an important concept of modern physics. The earliest is M. Prank proposed in 1900. He assumes that the radiation energy in the black body is discontinuous and can only take an integer multiple of the energy base unit. Later, research shows that not only the energy exhibits this discontinuous separation property, but other physical quantities such as angular momentum, spin, charge, etc. also exhibit this discontinuous quantization. This is a fundamental difference between the classic physics represented by Newtonia mechanics. Quantizic phenomena is mainly manifested in microscopic physical world. The physical theory describing the microscopic world is quantum mechanics.
