S rozvojem technologie výkonové elektroniky byly v průmyslové a zemědělské výrobě a přenosových zařízeních široce používány různé nelineární zátěže, díky nimž je zkreslení tvaru vlny elektrické sítě, tedy harmonické rušení, stále závažnější. Zkreslení průběhu elektrické sítě přinese mnoho škod, jako je zvýšení ztrát motorů, transformátorů, reaktorů atd., rušení komunikačních linek a způsobí částečnou nebo dokonce paralýzu celé energetické sítě. Pro lepší potlačení harmonických je nutné přesně analyzovat harmonické rušení elektrické sítě. V procesu vzorkování a diskretizace periodických signálů se obvykle používají dvě metody. Jedním z nich je kvazisynchronní vzorkování, které vyžaduje více průběhů a používá kvazisynchronní algoritmy k provádění velkého počtu iteračních operací, což není vhodné pro měření dynamických signálů; druhý je synchronní vzorkování, které se dělí na hardwarové synchronní vzorkování a softwarové synchronní vzorkování. Hardwarové synchronní vzorkování využívá obvod smyčky fázového závěsu, který je obecně komplikovaný v designu a nízké spolehlivosti; softwarové synchronní vzorkování nevyžaduje další hardwarové obvody a způsob jeho implementace je flexibilní. Byl široce používán při měření periodických signálů. Protože střídavý signál je speciální periodický signál, jeho spektrum je čárové spektrum rozložené na základní vlně a jejích celočíselných násobcích frekvence. Je nutné zajistit, aby vzorkovací signál a původní signál byly přísně synchronizovány, to znamená, že vzorkovací frekvence je celočíselný násobek frekvence signálu, jinak bude Výskyt úniku spektra je výsledkem diskrétní Fourierovy transformace signálu způsobují chyby testu a ovlivňují přesnost harmonické analýzy. Vzhledem k malým výkyvům ve frekvenci elektrické sítě je nevyhnutelné, že k výše uvedenému jevu dochází, když je vzorkovací frekvence pevná. Z tohoto důvodu domácí i zahraniční vědci navrhli mnoho metod, jak snížit vliv úniku spektra na přesnost měření.
Spektrální únik
Takzvaný spektrální únik označuje vzájemné ovlivňování mezi různými spektrálními čarami ve spektru signálu, což způsobuje, že se výsledek měření odchyluje od skutečné hodnoty a zároveň se objevuje na jiných frekvenčních bodech na obou stranách spektrální čáry. falešná spektra s menšími amplitudami. Jednoduše řečeno, příčinou úniku spektra je, že vzorkovací frekvence není synchronizována s frekvencí signálu, což způsobuje, že fáze periodického vzorkovacího signálu je na začátku a na konci nespojitá.
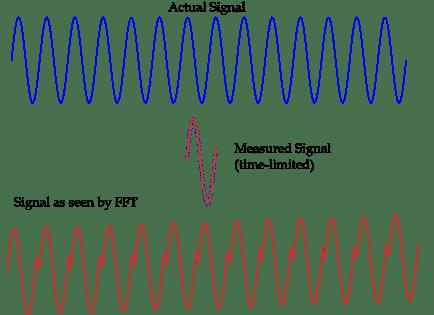
Takzvaný spektrální únik je vzájemné ovlivňování mezi různými spektrálními čarami ve spektru signálu, které způsobuje odchylku výsledku měření od skutečné hodnoty. Falešné spektrum. Použitím FFT k analýze harmonických v energetickém systému není možné vyhnout se problému úniku spektra. Je to způsobeno především inherentní nelinearitou, náhodností, distribucí, nestacionaritou a složitostí ovlivňujících faktorů. Frekvence není vždy konstantní hodnotou jmenovitého výkonu, bude se měnit v rozsahu kolem jmenovitého výkonu, takže nelze zaručit, že frekvence v reálném čase je celočíselný násobek základní frekvence, a synchronní vzorkování nelze dosáhnout. .
Metody pro potlačení úniku spektra navrhované doma i v zahraničí
Nejpřímějším dopadem úniku spektra je nepřesnost harmonické analýzy, která zase vede k nepřesnému měření elektrických parametrů na základě harmonické analýzy. přesný. Zvýšením počtu bodů vzorkování dat lze snížit únik, jehož podstatou je zmenšení šířky hlavního laloku obdélníkového okna. Zvýšení vzorkovací frekvence signálu může také snížit únik. Ve srovnání se zvýšeným objemem zpracování dat mají výše uvedené dvě metody extrémně omezené zlepšení úniku. Literatura navrhuje okenní funkce a interpolační techniky. Základním principem výběru funkce okna je požadavek úzkého hlavního laloku a malého bočního laloku, aby bylo možné tyto dva požadavky co nejvíce zohlednit, a obvykle se volí Hanningovo okno. Z časové oblasti se přidáním Hanningova okna ve skutečnosti stane fáze počátečního a koncového bodu periodického vzorkovacího signálu 0, což překonává jev, že fáze vzorkovacího signálu je nespojitá na začátku a na konci kvůli kolísání frekvence. , ale jakákoliv funkce okna nemůže vyřešit chybu způsobenou odchylkou nulového bodu na hlavním laloku, takže snížení úniku je také omezené. Interpolační technologie může téměř úplně eliminovat vliv úniku, ale objem zpracování dat tohoto algoritmu je příliš velký a výkon v reálném čase je obtížné zaručit. Literatura navrhuje algoritmus pro snížení úniku spektra. Jeho jádrem je, že když je součin vzorkovací periody a počtu vzorkovacích bodů roven celočíselnému násobku periody signálu, je diskrétní posloupnost získaná algoritmem vzorkovací posloupností signálu. Jinak algoritmus automaticky upraví vzorkování. sekvence. Simulace dokazuje, že algoritmus výrazněji zlepšuje únik spektra, když kolísání frekvence signálu není velké, a přesnost algoritmu je nižší, když je kolísání frekvence signálu velké. Obecným rysem výše uvedeného algoritmu je oprava vzorkovací sekvence nebo frekvenčního spektra, aniž by se řešila základní příčina úniku spektra. To určuje, že výše uvedený algoritmus nebo efekt není významný nebo že výkon v reálném čase je špatný. Základní příčinou úniku spektra je fs≠Nf0. Únik spektra lze efektivně vyřešit pouze úpravou fs v reálném čase tak, aby bylo fs=Nf0. Na základě výše uvedeného účelu je navržen algoritmus pro adaptivní úpravu vzorkovací frekvence a simulace prokazuje účinnost algoritmu.
Hlavním faktorem, který ovlivňuje rychlost tohoto algoritmu, je FFT. V posledních letech, se vznikem DSP čipů, které jsou zvláště vhodné pro zpracování dat a jejich aplikace v periodické analýze signálů, jsou operace FFT stále rychlejší. zcela vyhovující. Požadavky na systém v reálném čase. Proto má tento algoritmus velkou praktickou hodnotu v systému založeném na měření střídavého signálu. Algoritmus je v současné době aplikován na návrh monitorovacího systému vodních elektráren.
Únik spektra v profilometrii Fourierovy transformace
Fourierova transformační profilometrie (FTP) je běžně používaná metoda trojrozměrného měření povrchu. Jeho pracovní princip se skládá z následujících tří částí: 1) Tvar povrchu zkoušeného trojrozměrného objektu prostorově moduluje strukturované světelné pole mřížky tak, že deformované strukturované světelné pole nese informaci o výškovém rozložení tří objektů. -rozměrný tvar povrchu; 2) Pro spojitou distribuci Deformované strukturované světelné pole je vzorkováno pro získání diskrétních informací pro snadné počítačové zpracování; 3) Počítač provede Fourierovu transformaci na získané diskrétní informaci, vybere vhodné okno filtru pro odfiltrování složky základní frekvence ze spektra a obrátí složku základní frekvence. Fourierova transformace obnovuje výškové rozložení měřeného povrchu.
Když se Fourierova transformace provádí na diskrétním deformovaném strukturovaném světelném poli, algoritmus diskrétní Fourierovy transformace vyžaduje periodické rozšiřování deformovaného strukturovaného světelného pole v prostorové doméně. Prodloužení periody může způsobit únik spektra, takže při měření profilometrie Fourierovou transformací budou zavedeny chyby, ale jen málokdo o tom teoreticky diskutuje. Aby se snížil únik spektra způsobený expanzí periody, lidé často volí vhodnou okénkovou funkci (jako je Hanningovo okénko) ke zvážení deformovaného světelného pole, takže deformované světelné pole vzorkované CCD je zpracováno okénkovou funkcí a intenzita hrany okna je 0 a pak Fourierova transformace. Po zpracování signálu funkcí okna však dojde ke ztrátě některých informací, což je ekvivalentní snížení úniku spektra a zároveň vnesení chyb. Tento článek analyzuje problém úniku spektra deformovaného světelného pole s omezeným prostorem. Teoreticky je odvozen vztah mezi prodlouženou periodou a únikem spektra optického pole deformované struktury a je uveden způsob výpočtu a kvantitativní analýza chyby. Je zdůrazněno, že pouze když je expanzní perioda rovna celočíselnému násobku periody mřížky, jsou rozšířené proužky spojité a Fourierova transformace nezpůsobuje únik spektra; když doba expanze není rovna celočíselnému násobku periody mřížky, jsou rozšířené proužky nespojité. Zejména když je rozdíl 0,5 periody mřížky mezi periodou expanze a celočíselným násobkem periody mřížky deformovaného světelného pole, je porušení proužků po expanzi nejzávažnější a únik spektra je největší. Proto se při měření profilometrií s Fourierovou transformací snažte zvolit expanzní periodu rovnou celočíselnému násobku periody signálu, abyste snížili chybu měření způsobenou únikem spektra. Pokud to není možné, lze použít iterační metodu k extrapolaci proužků, aby se vytvořily nové proužky na obou stranách efektivního zorného pole, aby se chyba úniku rozšířila za efektivní zorné pole a snížila se chyba okrajového úniku.
