Úvod do problému
18. století Gobini, je zde řeka, jsou zde dva ostrovy, existuje sedm mostů spojujících dva ostrovy s břehem řeky (např. obrys mapy). Někteří lidé navrhli otázku: Jak může chodec neopakovat, neminout sedm mostů najednou a nakonec se vrátit do výchozího bodu. Později to velký matematik Euli přeměnil v geometrickou záležitost – problém malby. Nejenže tento problém vyřešil, ale také vyplnil tabulku obrázku: Počet lichých bodů není 0 je 2 (sudý počet lichých čísel, "pokud je Sudé číslo se nazývá sudé. chcete nakreslit obrázek, musíte mít uprostřed sudou věc, to znamená, že existuje jiný způsob, jak mít jiný způsob, a singularita může být pouze na obou koncích, takže lze nakreslit jakoukoli postavu, Měli jste nebo na oba konce).
Inferenční metoda
Když Euler navštívil pruský Gobisburg (nyní Rusko Galoningrad), našel velmi zajímavou místní veřejnost. Konfuciovat. V Gobinic City je řeka zvaná Pregel, tato zajímavá zábava je sobotní procházka ze všech sedmi mostů a každý most může projít pouze jednou a výchozí bod musí být stejné místo. .
Euchi vloží každý kus do bodu, který spojí dva pozemské mosty.
Takovým způsobem není možné se dotazovat. Jeho argument je ten, že kromě výchozího bodu pokaždé, když člověk vstoupí do země (nebo bodu) mostem, také tento bod opustí jiným mostem. Každá čára je tedy v bodě, dva mosty (nebo čáry) se počítají z čáry od počátečního bodu a čáry posledního vratného bodu, takže počet mostů připojených k dalšímu pozemku je téměř sudý.
Vyskytl se problém
Sedmý most, není zde žádný bod obsahující počet orientací, takže výše uvedené úkoly nelze splnit.
Euler je velmi důležitý, je také velmi chytrý, ukazuje jedinečnost matematika zabývajícího se praktickými problémy - abstrahuje aktuální problém do vhodného "matematického modelu". Tato výzkumná metoda je "Metoda matematického modelu". To nemusí používat jak hlubokou teorii, ale myslete na to, ale na klíč k vyřešení problému.
Dále Euler použije malbu na obrázku k posouzení pokynů a rychle usoudil, že 7 mostů, které neopakují přístav Doinsburg ani jednou. Jinými slovy, kolik let přijde, lidé věnují pozornost neopakující se trase, vůbec neexistují. Problém, který bylo těžké žít, je vlastně taková náhradní odpověď!
Konečný úspěch
Počáteční období problému
Po vznesení otázky se o to mnoho lidí velmi zajímá, ale experimentují, ale po dlouhé době jsem se nikdy nevyřešil. S běžnými matematickými znalostmi se každý most vezme jednou a všech sedm mostů ujde celkem 5040, a tak mnoho případů, bude to zkouška, což bude hodně práce. Jak ale najdu cestu, která úspěšně prochází každým mostem, místo aby se opakovala? Vzniká tak slavný „gossoburský problém sedmi mostů“.
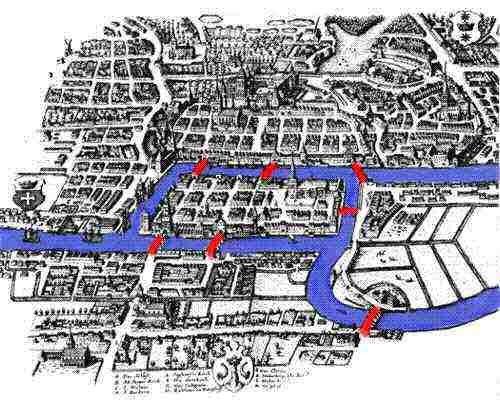
Problém Po expozici
V roce 1735 píše několik vysokoškolských studentů dopis geniálnímu matematikovi Eurovi, který pracuje v Rusku, Porsopian Academy of Sciences. Požádejte ho, aby pomohl vyřešit tento problém. Pozoroval jsi Tvrdý most v Gobi a vážně o tom přemýšlel, ale nebyl schopen uspět, takže měl podezření, že otázka Qiqiao to nevyřešila?
V roce 1736, po roce výzkumu, 29letý Orap předložil dokumenty „Gobi Seven Bridge“, úspěšně tento problém vyřešil a vytvořil nové odvětví matematiky -- Teorie grafů.
V tomto článku Eutu abstrahuje problém Qiqiao a vezme každý kus do bodu, spojí dva pozemní mosty. A tím získal stejnou geometrii, jak je znázorněno. Pokud použijeme A, B, C, D čtyři body k reprezentaci čtyř oblastí Gobinic. Takový slavný „problém sedmi mostů“ je převeden na to, zda je možné použít neopakující se malbu sedmi čar. Pokud umíte kreslit, musíte mít v grafice koncové a počáteční body a počáteční a koncový bod by měly být stejné. Vzhledem k tomu, že symetrie může být viděna z B nebo C jako počáteční bod, pokud se předpokládá, že A je počáteční a koncový bod, pak musí být jeden od drátu a odpovídající vstupní čáry. Pokud definujeme počet řad čáry vstupující do A, počet řad, které opouštějí drát, je výstupní a počet tyčí čáry je stupeň A, pak a Stupeň a stupeň stupňů jsou stejné, to znamená, že stupeň A by měl být sudé číslo. To znamená, že je nutné udělat decizor z A. Degilita degility by měla být sudé číslo a stupeň ve skutečnosti A je 5 lichý, takže je vidět, že je od A nepodřaditelné. čas, pokud je z B nebo D, protože stupně B, D jsou 3, 3, každý je lichý, to znamená, že výchozí bod není zveřejněn.
Je známo, že výše uvedený důvod spočívá v tom, že abstraktní matematický problém je nesubalyptovaný, tj. "sedm můstkových úloh" také není publikováno.
From this we get: Euler loop relationship
Můžeme tedy vědět, že grafiku A lze kreslit, musí splňovat následující dvě podmínky:
1. Grafika musí být připojena.
2. Počet "kurzů" na obrázku je 0 nebo 2.
Můžeme také ověřit, že grafiku lze kreslit. Může být také posouzen k posouzení "sedm problémů mostu", 4 body jsou liché, může vědět, že obrázek nelze "nakreslit", to znamená, že neexistuje opakovaně projít všech sedm mostů.
V roce 1736 Eucula vysvětlil svou metodu řešení v dokumentech „Mostu Gobinburg 7“, které byly předány petrohradské akademii. Jeho indukce, položení základu pro nové matematické odvětví - ustavení topologie.
Otázka Qiqiao a Eulerova věta
Euler přejímá výzkum týkající se problému Qiqiao, nejen proto, aby zopakoval problém navržený obyvateli Gobinburgu a získal a dokázal tři závěry týkající se mrtvice a lidé jsou často nazýváni Eulerovou větou. Pro spojovací mapu se obvykle nazývá Euler Road z trasy, která je nakreslena z uzlu. Lidé obvykle nazývají dvojici Eulerových obvodů, které jsou taženy zpět do výchozího bodu. Obrázek s evropskou smyčkou se nazývá Eulerova mapa.
Toto téma je obsaženo ve 12. knize Matematika Matematika. 104 stran.
Toto téma je obsaženo i v prvním díle prvního dílu. Na straně 121.
Malba
⒈⒈⒈ ⒈ 通 通 通 图 图 图 图 图 图 图 图 图 图 图 通 图 图 图 图 图 图 图When you draw, you can take anything at the starting point, and finally you can draw this picture with this point.
⒉ Tam, kde jsou pouze dvě liché perspektivy (zbytek je sudý), musí být nakreslen. Když kreslíte, musíte zadat podivný bod jako počáteční bod a další lichý bod je konec.
⒊ Jiné stavové mapy nelze kreslit. (Počet lichých bodů lze vypočítat na druhém obrázku a nakreslit několik kusů.)
