Historické pozadí
Více než půl století před narozením Maxwella udělali lidé velký pokrok v chápání elektromagnetických jevů. V roce 1785 francouzský fyzik C. A. Coulomb (Charles A. Coulomb) na základě výsledků experimentu torzní rovnováhy stanovil Coulombův zákon popisující interakční sílu mezi dvěma bodovými náboji. V roce 1820 H. C. Oersted (Hans Christian Oersted) zjistil, že elektrický proud může vychylovat magnetické jehly, a tím spojovat elektřinu s magnetismem. Poté A. M. Ampère (Andre Marie Ampère) studoval interakci mezi elektrickými proudy a předložil mnoho důležitých pojmů a zákon Amperovy smyčky. M. Faraday (Michael Faraday) významně přispěl v mnoha aspektech, zejména v zákoně elektromagnetické indukce publikovaném v roce 1831, který je důležitým teoretickým základem pro motory, transformátory a další zařízení.
V roce 1845 byly shrnuty tři nejzákladnější experimentální zákony o elektromagnetických jevech: Coulombův zákon (1785), Biot-Savartův zákon (1820), Faradayův zákon elektromagnetické indukce (1831 ~ 1845) ), Faradayovy pojmy „siločáry“. " a "čára magnetické síly" (nyní také nazývaná "čára elektrického pole" a "čára magnetické síly") byly vyvinuty do "pojmu elektromagnetického pole". Od roku 1855 do roku 1865 Maxwell komplexně zhodnotil Coulombův zákon, Biot-Savartův zákon a Faradayův zákon a přinesl metody matematické analýzy do oblasti elektromagnetického výzkumu, což vedlo ke zrodu Maxwellovy elektromagnetické teorie. .
Před Maxwellem byly všechny teorie o elektromagnetických jevech založeny na konceptu akce na velkou vzdálenost. Předpokládalo se, že interakce mezi nabitými tělesy, zmagnetizovanými tělesy nebo vodiči s proudem může být prováděna přímo za středním prostředím. A to se děje okamžitě, to znamená, že rychlost šíření elektromagnetického rušení je považována za nekonečnou. V té době měl pouze Faraday odlišné názory. Domnívá se, že výše uvedené interakce souvisejí s intermediálními médii a jsou prováděny prostřednictvím přenosu intermediálních médií, tedy zastává teorii nepřímého přenosu.
Maxwell zdědil Faradayův pohled, odvolával se na model mechaniky tekutin, aplikoval rigorózní matematické formy ke shrnutí práce předchůdců, navrhl hypotézu posuvného proudu, rozšířil význam proudu a uzavřel základní zákony elektromagnetického pole Existují čtyři diferenciální rovnice, což jsou slavné Maxwellovy rovnice. Analyzoval tento soubor rovnic, předvídajících existenci elektromagnetických vln, a dospěl k závěru, že rychlost šíření elektromagnetických vln je konečná hodnota (blízká rychlosti světla) a že světlo je také elektromagnetická vlna určité frekvence. Vše výše uvedené napsal ve svém článku nazvaném „O elektřině a magnetismu“.
V roce 1887 použil Heinrich R. Hertz experimentální metody ke generování a detekci elektromagnetických vln, což potvrdilo Maxwellovu předvídavost. V letech 1905 až 1915 teorie relativity Alberta Einsteina dále prokázala vztah mezi časem, prostorem, hmotou, energií a pohybem, což naznačuje, že elektromagnetická pole jsou formou hmoty a byla uznána teorie nepřímosti.
Složení rovnice
Maxwellovy rovnice se skládají ze čtyř rovnic:
Gaussův zákon: Tento zákon popisuje vztah mezi elektrickým polem a rozložením náboje v prostoru. Siločáry elektrického pole začínají kladným nábojem a končí záporným nábojem (neboli nekonečnem). Vypočítejte počet siločar elektrického pole procházejících danou uzavřenou plochou, tedy její elektrický tok, a můžete znát celkový náboj obsažený v této uzavřené ploše. Tento zákon podrobněji popisuje vztah mezi elektrickým tokem procházejícím libovolnou uzavřenou plochou a nábojem v uzavřené ploše.
Gaussův magnetický zákon: Tento zákon ukazuje, že magnetické monopóly ve skutečnosti neexistují. Proto neexistuje žádný izolovaný magnetický náboj a siločára magnetického pole nemá žádný počáteční bod a žádný koncový bod. Magnetické siločáry se budou smyčkovat nebo prodlužovat do nekonečna. Jinými slovy, siločáry magnetického pole vstupující do jakékoli oblasti musí tuto oblast opustit. V terminologii je magnetický tok procházející jakýmkoli uzavřeným povrchem roven nule, neboli magnetické pole je pole pasivní.
Faradayův zákon indukce: Tento zákon popisuje, jak časově proměnné magnetické pole indukuje elektrické pole. Elektromagnetická indukce je teoretickým základem pro výrobu mnoha generátorů. Například rotující tyčový magnet generuje časově proměnlivé magnetické pole, které zase generuje elektrické pole, což způsobuje, že sousední uzavřený obvod indukuje proud.
Maxwell-Amperův zákon: Tento zákon říká, že magnetické pole lze generovat dvěma způsoby: jedním je vedení proudu (původní Ampérův zákon) a druhým je časově se měnící elektrické pole nebo posunový proud (Maxwellův korekční člen) .
V elektromagnetice Maxwellův korekční termín znamená, že časově proměnlivé elektrické pole může generovat magnetické pole a díky Faradayovu zákonu indukce může časově proměnlivé magnetické pole generovat elektrické pole. Tímto způsobem dvě rovnice teoreticky umožňují šíření samoudržujících se elektromagnetických vln v prostoru.
Hlavní body Maxwellovy teorie elektromagnetického pole lze shrnout takto:
①Několik diskrétních nabitých objektů nebo proudů, všechny elektrické a magnetické interakce mezi nimi jsou přenášeny mezi nimi Co je přenášeno ve střední oblasti, bez ohledu na to, zda je střední oblastí vakuum nebo fyzická látka.
②Elektrická energie nebo magnetická energie neexistuje pouze v nabitých tělech, zmagnetizovaných tělech nebo nabitých předmětech, ale většina z nich je distribuována v okolním elektromagnetickém poli.
③Pokud dojde k přerušení v obvodu tvořeném vodičem, vodivý proud v obvodu bude kompenzován posuvným proudem v dielektriku, to znamená, že plný proud je spojitý. A vztah mezi posuvným proudem a magnetickým polem, které generuje, je stejný jako vztah vodivostního proudu.
④ Magnetický tok nemá začátek ani konec, to znamená, že neexistuje žádný magnetický náboj.
⑤Světelné vlny jsou také elektromagnetické vlny.
Maxwellovy rovnice lze vyjádřit dvěma způsoby.
1. Integrální tvar Maxwellových rovnic je matematický model, který popisuje elektromagnetické pole v určitém objemu nebo ploše. Výraz je:
Equation ① is the law of total current derived from the generalization of the law of Ampere’s loop, and its meaning is: the line integral of the magnetic field intensity H along any closed curve is equal to the area passing through the limited area of this curve Full current. The first term on the right side of the equal sign is the conduction current. The second term is the displacement current. Equation ② is the expression of Faraday's law of electromagnetic induction, which shows that the line integral of the electric field intensity E along any closed curve is equal to the negative value of the rate of change of the magnetic flux passing through the area defined by the curve with respect to time. The closed curve mentioned here does not necessarily have to be composed of conductors, it can be a dielectric loop, or even just any closed contour. Equation ③ represents the principle of magnetic flux continuity, indicating that for any closed curved surface, as much magnetic flux enters the curved surface, the same amount of magnetic flux leaves. That is to say, the B line has neither a beginning nor a terminal; it also shows that there is no magnetic charge corresponding to the electric charge. Equation ④ is the expression of Gauss's law, which shows that under time-varying conditions, the net flux of D from any closed surface should be equal to the sum of all free charges in the volume enclosed by the closed surface.
2. Maxwellovy rovnice v diferenciálním tvaru. Diferenciální tvar Maxwellových rovnic je pro každý bod v poli. Pomocí operátoru del je lze zapsat jako
Rovnice ⑤ je diferenciální tvar zákona o celkovém proudu, který ukazuje, že zvlnění intenzity magnetického pole H se rovná celkové hustotě proudu v tomto bodě (hustota vodivého proudu J a hustota posuvného proudu The sum), tj. vírovým zdrojem magnetického pole je plná proudová hustota a posuvný proud může generovat magnetické pole stejně jako vodivostní proud. Vzorec ⑥ je diferenciální tvar Faradayova zákona elektromagnetické indukce, který ukazuje, že stočení intenzity elektrického pole E se rovná záporné hodnotě časové rychlosti změny hustoty magnetického toku B v tomto bodě, tj. vírový zdroj elektrického pole je časová rychlost změny hustoty magnetického toku. Rovnice ⑦ je diferenciální forma principu spojitosti magnetického toku, která ukazuje, že divergence hustoty magnetického toku B je vždy rovna nule, to znamená, že čára B nemá začátek ani konec. To znamená, že neexistuje žádný magnetický náboj odpovídající elektrickému náboji. Rovnice ⑧ je zobecněním Gaussova zákona elektrostatického pole, to znamená, že za časově proměnných podmínek je divergence elektrického posunutí D stále rovna hustotě volného náboje v tomto bodě.
Kromě výše uvedených čtyř rovnic je vyžadován konstitutivní vztah média
konečně vyřešit problém řešení polní veličiny. Kde ε je dielektrická konstanta média, μ je propustnost média a σ je vodivost média.
Formulář výrazu
Integrální forma
Integrální tvar Maxwellových rovnic je následující:
To je rok 1873 Kolem roku Maxwell navrhl čtyři rovnice vyjadřující univerzální zákon elektromagnetických polí. Mezi nimi:
(1) popisuje povahu elektrického pole. Obecně může být elektrické pole elektrické pole s volným nábojem nebo indukované elektrické pole vybuzené měnícím se magnetickým polem a indukované elektrické pole je vírové pole a jeho elektrická posuvná čára je uzavřená a nepřispívá k toku. uzavřeného zakřiveného povrchu.
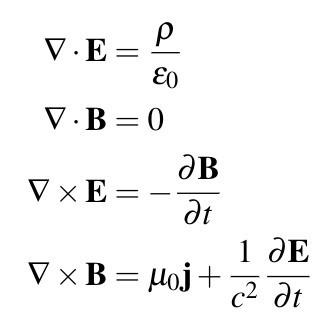
(2) popisuje povahu magnetického pole. Magnetické pole může být vybuzeno vodivým proudem nebo posuvným proudem měnícího se elektrického pole. Jejich magnetická pole jsou všechna vírová pole a magnetické indukční čáry jsou uzavřené čáry, které nepřispívají k toku uzavřeného zakřiveného povrchu.
(3) popisuje zákon měnícího se magnetického pole pro vybuzení elektrického pole.
(4) popisuje zákon vedení proudu a změny elektrického pole pro vybuzení magnetického pole.
Formulář ve stabilním poli
Když
, rovnice jsou redukovány na rovnice elektrostatického pole a ustáleného magnetického pole:
Formujte ve volném prostoru bez zdroje pole
Když, the equation system becomes the following form:
The integral form of Maxwell's equations reflects the relationship between the amount of electromagnetic field (D, E, B, H) and the field source (charge q, current I) in a certain area of space.
Diferenciální forma
Při vlastní aplikaci elektromagnetického pole je často nutné znát vztah mezi množstvím elektromagnetického pole bod po bodu v prostoru a nábojem a proudem. Z matematického tvaru se integrální tvar Maxwellových rovnic převádí do diferenciálního tvaru. Obrácený trojúhelník je Hamiltonián.
Poznámka:
(1) V různých inerciálních vztažných soustavách mají Maxwellovy rovnice stejný tvar.
(2) Aby bylo možné použít Maxwellovy rovnice k řešení praktických problémů, je třeba vzít v úvahu také vliv prostředí na elektromagnetické pole. Například v rovnoměrném a izotropním médiu má množství elektromagnetického pole následující vztah s charakteristikami média:
V nestejnoměrném médiu by měla být hraniční hodnota množství elektromagnetického pole na rozhraní také považována za vztah. Pomocí podmínky počáteční hodnoty veličiny pole, kdy t=0, lze v zásadě získat elektromagnetické pole v libovolném bodě prostoru v libovolném čase, a to E(x, y, z, t) a B(x, y, z, t).
Níže jsou uvedeny Maxwellovy rovnice v systému Gaussových jednotek
Rovnice fyzikálních vlastností
Když there is a medium, due to electric and magnetic fields The interaction with the medium makes the amount of electromagnetic field related to the characteristics of the medium. Therefore, the above-mentioned Maxwell equations are not complete at this time, and the physical property equations describing the properties of the medium (isotropic medium) need to be supplemented, respectively
Ve vzorci jsou ε, μ a σ absolutní dielektrická konstanta, absolutní permeabilita a vodivost vodiče, respektive Rate.
Další teoretický důkaz, že Maxwellovy rovnice a rovnice fyzikálních vlastností dohromady jsou kompletní sadou rovnic pro určování změn elektromagnetického pole. To znamená, že když je dán náboj a proud, lze z výše uvedené rovnice zcela určit změnu elektromagnetického pole podle počátečních podmínek (a nezbytných okrajových podmínek). Samozřejmě, pokud chcete diskutovat o vlivu elektromagnetického pole na nabité částice a pohyb nabitých částic v elektromagnetickém poli, potřebujete také vzorec Lorentzovy síly.
Formulář komplexního čísla
Pro sinusová časově proměnná pole lze použít komplexní vektory k vyjádření zákona o elektromagnetických polích jako komplexní čísla.
V zákoně komplexního elektromagnetického pole, protože komplexní veličina pole a zdrojová veličina jsou pouze funkcemi prostorové polohy, není při řešení nutné uvažovat jejich závislost na čase. Proto je vhodnější použít komplexní zákon elektromagnetického pole k diskusi o sinusovém časově proměnlivém poli.
Poznámky
Pomocí různých jednotkových systémů se tvar Maxwellových rovnic mírně změní a obecný tvar je stále stejný, ale na různých pozicích v rovnici se objeví různé konstanty.
Mezinárodní systém jednotek je nejběžněji používaný jednotkový systém. Celý strojírenský obor využívá tento jednotkový systém. Většina chemiků také používá tento jednotkový systém. Téměř všechny vysokoškolské učebnice fyziky používají tento systém jednotek. Systém. Další běžně používané jednotkové systémy jsou jednotky Gauss, Lorentz-Heaviside a Planck. Gaussův jednotkový systém odvozený od systému centimetr-gram-sekunda je vhodnější pro účely výuky a může rovnice vypadat jednodušší a srozumitelnější. Jednotkový systém Lorentz-Heaviside je také odvozen od systému centimetr-gram-sekunda a používá se hlavně v částicové fyzice; Planckův jednotkový systém je přirozený jednotkový systém a jeho jednotky jsou definovány podle povahy přírody. Nastaveno člověkem. Systém Planckových jednotek je velmi užitečným nástrojem pro studium teoretické fyziky a může poskytnout velké osvícení. Na této stránce, pokud není uvedeno jinak, jsou všechny rovnice v Mezinárodní soustavě jednotek.
Zde jsou uvedeny dva ekvivalentní výrazy Maxwellových rovnic. První výraz je následující:
Tento výraz přičte volný náboj a vázaný náboj k celkovému náboji požadovanému Gaussovým zákonem a také vydělí volný proud, vázaný proud a polarizační proud. Součet je celkový proud podle Maxwell-Ampereova zákona. Tento výraz zaujímá relativně základní a mikro hledisko. Tento výraz lze použít k výpočtu elektrických a magnetických polí generovaných nábojem z konečného zdroje a zdrojovým proudem ve vakuu. Ve skutečnosti je však ve hmotě příliš mnoho elektronů a atomových jader, které nelze do výpočtu zahrnout. Ve skutečnosti klasický elektromagnetismus nepotřebuje tak přesné odpovědi.
Pro druhý výraz se prosím podívejte na "obecnou formu" ve výše uvedeném "integračním formuláři". Jako zdroj bere volný náboj a volný proud a nepočítá přímo příspěvek vázaného náboje objevujícího se v dielektriku a vázaného proudu a polarizačního proudu objevujícího se v magnetizované látce. Protože v obecných skutečných podmínkách jsou parametry, které lze přímo řídit, volný náboj a volný proud, a vázaný náboj, vázaný proud a polarizační proud jsou jevy, ke kterým dochází poté, co je látka polarizována. Použití tohoto výrazu usnadní dielektrikum nebo magnetizaci Různé fyzikální výpočty v látce jsou jednodušší.
Na povrchu se zdá, že Maxwellovy rovnice jsou přeurčené. Má pouze šest neznámých (vektorové elektrické pole a magnetické pole má každý tři neznámé, proud a náboj neznámé nejsou. Je to fyzikální veličina, která je volně daná a odpovídá zachování náboje), ale existuje osm rovnic (dvě Gaussovy zákony mají dvě rovnice, Faradayův zákon a Ampérův zákon jsou vektorové, každý obsahuje tři rovnice). Tato situace souvisí s omezenou opakovatelností Maxwellových rovnic. Z teorie lze odvodit, že každý systém, který splňuje Faradayův zákon a Amperův zákon, musí splňovat dva Gaussovy zákony.
Na druhou stranu Maxwellovy rovnice nejsou uzavřené. Pouze s ohledem na vlastnosti elektromagnetického prostředí může tento systém rovnic získat konečné řešení.
Použitelné měřítko
The Maxwell equations are usually applied to the "macro average field" of various fields. Když the scale shrinks to the microscopic scale, so as to approach the size of a single atom, the local fluctuations of these fields will become unignorable, and quantum phenomena will begin to appear. Only under the premise of macro-average, some physical quantities such as the permittivity and permeability of a substance can get meaningful definition values.
Poloměr nejtěžšího jádra je asi 7 femtometrů (1fm=10-15m). Proto se v klasické elektromagnetice mikroskopické měřítko vztahuje na řádově větší než 10-14m. Aby se splnilo mikroskopické měřítko, elektrony a jádra mohou být považovány za bodové náboje a jsou stanoveny mikroskopické Maxwellovy rovnice; jinak je třeba vzít v úvahu rozložení náboje uvnitř jádra. Elektrické a magnetické pole vypočtené v mikroskopickém měřítku se stále dost drasticky mění, vzdálenost prostorové změny je menší než 10-10m a doba změny času je mezi 10-17 a 10-13 sekundami. Proto z mikroskopických Maxwellových rovnic musí být provedena klasická operace průměrování, aby se získalo hladké, spojité a pomalu se měnící makroskopické elektrické pole a makroskopické magnetické pole. Nejnižší hranice makro měřítka je 10-8 metrů. To znamená, že chování odrazu a lomu elektromagnetických vln lze popsat makro-Maxwellovými rovnicemi. Vezmeme-li tento minimální limit jako délku strany, krychle o objemu 10-24 metrů krychlových obsahuje přibližně 106 jader a elektronů. Fyzikální chování tolika jader a elektronů po klasickém zprůměrování stačí k vyhlazení jakýchkoli prudkých výkyvů. Podle spolehlivých literárních záznamů vyžaduje klasická operace průměrování pouze průměrování v prostoru, nikoli v čase, a nemusí uvažovat kvantové efekty atomů.
Význam
Maxwellův příspěvek k vytvoření konceptu pole je také velkou inovací ve fyzice té doby, protože právě vznik konceptu pole přiměl mnoho fyziků Vědci se mohli zbavit okovů Newtonova „konceptu supervzdálenosti“ a obecně přijal myšlenku, že elektromagnetické a gravitační efekty jsou oba „blízkost“.
Pozice Maxwellových rovnic v elektromagnetice a klasické elektrodynamice je stejná jako pozice Newtonových pohybových zákonů v newtonovské mechanice. Elektromagnetická teorie zaměřená na Maxwellovy rovnice je jedním z nejpyšnějších úspěchů klasické fyziky. Dokonalá jednota elektromagnetické interakce, kterou odhalila, utvrdila fyziky v přesvědčení, že různé interakce hmoty by měly být sjednoceny na vyšší úrovni. Tato teorie je široce aplikována na technické obory.
Vědecký význam
(1) Klasickou teorii pole založil Maxwell na konci 19. století na základě shrnutí tří experimentálních zákonů elektromagnetického pole a jejich srovnání s mechanickými modely. Ale Maxwellův hlavní úspěch mu přesně umožnil vymanit se z omezení rámce klasické mechaniky: ve fyzice vzal jako základní výzkumný objekt „pole“ místo „síly“ a zavedl vektorovou parciální diferenciální operaci, která se liší od klasická matematika v matematice. Symbol. Tyto dva jsou základem pro objev rovnice elektromagnetických vln. To znamená, že Maxwellova práce ve skutečnosti prorazila rámec klasické fyziky a matematiky v té době, ale kvůli tehdejším historickým podmínkám mohou lidé stále rozumět teorii elektromagnetického pole pouze z rámce Newtonova počtu a klasické mechaniky. .
Moderní matematika, matematická analýza v Hilbertově prostoru se objevila až na přelomu 19. a 20. století. Pojem vlnění hmoty v kvantové mechanice byl objeven až později, zejména nerozlučné matematicko-logické spojení mezi moderní matematikou a kvantovou fyzikou nebylo dosud lidmi zcela pochopeno a přijato. Od Maxwellova založení teorie elektromagnetického pole až do současnosti lidé vždy používali klasickou matematiku v euklidovském prostoru jako základní metodu k řešení Maxwellových rovnic.
(2) Ze vzniku, formy, obsahu a historického procesu Maxwellových rovnic můžeme vidět: Za prvé, fyzický objekt se rozvine do nového axiomového výrazu na hlubší úrovni. Vědecký pokrok, který bude ovládán lidstvem, se nebude vyvíjet podle zavedených předpokladů. Zavedení nového axiomového systému s kognitivním významem je známkou vědeckého teoretického pokroku. Zadruhé, ačkoli fyzický objekt a způsob jeho vyjádření jsou různé věci, je nemožné rozpoznat „existenci“ tohoto objektu, aniž bychom se spoléhali na správnou metodu vyjádření. Za třetí, teorie, kterou budujeme, bude určovat úroveň významu, ve kterém děláme z našich objektů fyzikální fakta. To je přesně ten zmatek, který nám přináší moderní špičková fyzika.
(3) Maxwellovy rovnice odhalují krásu symetrie ve vzájemné transformaci elektrických a magnetických polí. Tato krása je plně vyjádřena v moderní matematické formě. Na jedné straně bychom však měli připustit, že pouze správný matematický tvar může plně demonstrovat integritu (elektromagnetickou symetrii), kterou nelze vidět v empirické metodě; na druhou stranu bychom neměli zapomínat, že krása této symetrie je v matematické podobě. Jednotná povaha elektromagnetického pole se odráží. Proto bychom si měli uvědomit, že tuto symetrii bychom měli „objevit“ nebo „vidět“ v matematických výrazech, než přímo vyvozovat tuto podstatu z fyzikálních matematických vzorců.
