Základní znalosti
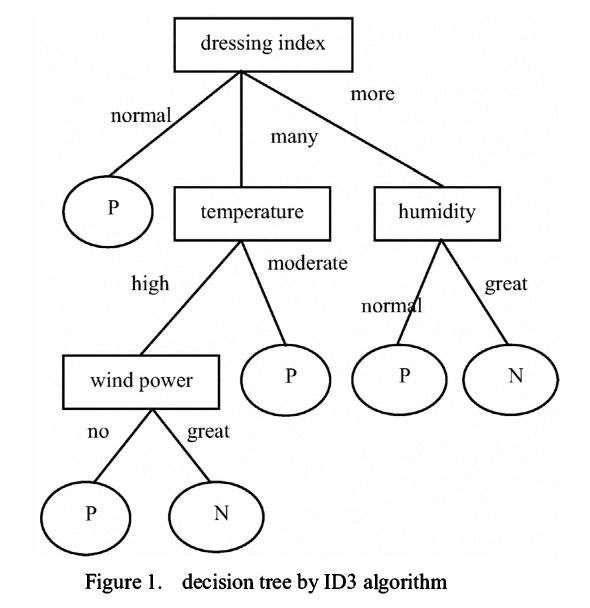
TheAlgoritmus ID3wasfirstproposedbyJ.RossQuinlanattheUniversityofSydneyin1975asaclassificationpredictionalgorithm.Thecoreofthealgorithmis"informationentropy"..TheAlgoritmus ID3calculatestheinformationgainofeachattributeandconsidersthattheattributewithhighinformationgainisagoodattribute.Eachtimetheattributewiththehighestinformationgainisselectedasthepartitionstandard,thisprocessisrepeateduntiladecisiontreethatcanperfectlyclassifytrainingexamplesisgenerated.
Decisiontreeistoclassifydatatoachievethepurposeofprediction.Thedecisiontreemethodfirstformsadecisiontreebasedonthetrainingsetdata.Ifthetreecannotgivethecorrectclassificationtoallobjects,selectsomeexceptionstoaddtothetrainingsetdata,andrepeattheprocessuntilthecorrectdecisionsetisformed.Thedecisiontreerepresentsthetreestructureofthedecisionset.
Thedecisiontreeiscomposedofdecisionnodes,branchesandleaves.Thetopnodeinthedecisiontreeistherootnode,andeachbranchisanewdecisionnode,oraleafofthetree.Eachdecisionnoderepresentsaproblemordecision,andusuallycorrespondstotheattributesoftheobjecttobeclassified.Eachleafnoderepresentsapossibleclassificationresult.Intheprocessoftraversingthedecisiontreefromtoptobottom,eachnodewillencounteratest,andthedifferenttestoutputsoftheproblemoneachnodewillleadtodifferentbranches,andfinallyaleafnodewillbereached.ThisprocessItistheprocessofusingdecisiontreestoclassify,usingseveralvariablestodeterminethecategoryitbelongsto.
Algoritmus ID3
TheAlgoritmus ID3wasfirstproposedbyQuinlan.Thealgorithmisbasedoninformationtheory,andusesinformationentropyandinformationgainasmeasurementstandards,soastorealizetheinductiveclassificationofdata.Thefollowingaresomebasicconceptsofinformationtheory:
Definice1:Pokud se objeví zprávy se stejnou pravděpodobností, pravděpodobnost každé zprávy je1/n a množství informací přenášených zprávou je-Log2(1/n)
Definice2:Pokud se objeví zprávy a dané rozdělení pravděpodobnosti je P=(p1,p2...pn), pak se množství informací přenášených rozdělením nazývá entropie P.For
.
Definice 3:Pokud je sada záznamů rozdělena do nezávislých kategoriíC1C2..Ckapodlehodnotyatributukategorie,množství informací potřebných k určení,kterákategorieprvkuTpatříkInfo(T)=I(p),kdePisthepravděpodobnostrozděleníC|,T|C2,(P|)...
Definition4:IfWefirstdivideTintosetsT1,T2...Tnaccordingtothevalueofthenon-categoryattributeX,andthendeterminetheamountofinformationofanelementclassinTcanbeobtainedbydeterminingtheweightedaveragevalueofTi,thatis,theweightedaveragevalueofInfo(Ti)is:
Info(X,T)=(i=1tuna)((|Ti|/|T|)Info(Ti))
Definition5:InformationGainisthedifferencebetweentwoamountsofinformation.OneamountofinformationistheamountofinformationofoneelementofTthatneedstobedetermined,andtheotheramountofinformationistheamountofinformationofoneelementofTthatneedstobedeterminedafterthevalueofattributeXhasbeenobtained.Theinformationgaindegreeformulais:
Zisk(X,T)=Info(T)-Info(X,T)
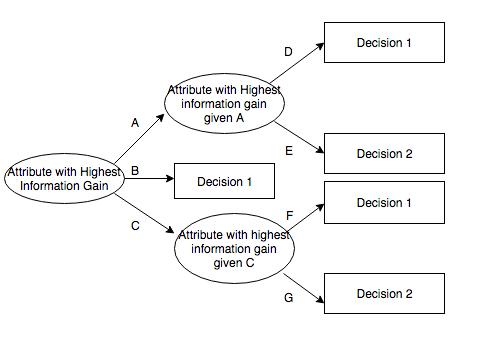
Algoritmus ID3calculatestheinformationgainofeachattribute,Andselecttheattributewiththehighestgainasthetestattributeofthegivenset.Createanodefortheselectedtestattribute,markitwiththeattributeofthenode,createabranchforeachvalueoftheattributeanddividethesampleaccordingly.
Popis dat
Použitá vzorová data mají určité požadavky. ID3 je:
Description-attribute-attributeswiththesamevaluemustdescribeeachexampleandhaveafixednumberofvalues.
Předdefinované atributy instance třídy musí být definovány, to znamená, že se neučí ID3.
Diskrétní třída – třída musí být ostrá a odlišná. Rozklad souvislých tříd do fuzzy kategorií (jako jsou kovy „tvrdé, obtížné, ohebné, jemné a měkké“ není věrohodné.
Enoughexamples-becauseinductivegeneralizationisusedfor(Thatis,itisnotpossibletofindout.)Enoughtestcasesmustbeselectedtodistinguishvalidpatternsandeliminatetheinfluenceofspecialcoincidencefactors.
Výběr atributu
ID3determineswhichattributesarebest.Astatisticalfeature,calledinformationgain,usesentropytoobtainagivenattributetomeasurethetrainingexamplesbroughtintothetargetclass.Theinformationwiththehighestinformationgain(informationisthemostusefulcategory)isselected.Inordertoclarifythegain,wefirstborrowfrominformationtheoryOnedefinitioniscalledentropy.Everyattributehasanentropy.
