Úvod
Binární číslo je přenášení přenášení, 0, 1 je základní operátor; počítačový operátor se používá binárně. Základem počítače je binární. Běžně navržený v raném designu je hlavně desítkový (protože máme deset prstů, je to rozumnější volba a prst může představovat deset čísel. 0 Koncept je, dokud se neobjeví na dlouhou dobu, takže je 1-10 Ne 0 -9). Poté, co se objeví elektronický počítač, se použití elektronek používá k označení, že deset stavů je příliš komplikovaných, takže existují pouze dva základní stavy, otevřený a vypnutý. To znamená, že dva stavy elektronky určují použití binárního systému pomocí binárních elektronických počítačů.
binární počet
čtyři operace
plus výpočet: 0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1, 1 + 1 = 10, všechny 2 do 1;
mínus operace: 1-1 = 0, 1-0 = 1, 0-0 = 0, 0-1 = 1, do horní polohy 1, když 2; < / p>
násobte: 0 × 0 = 0, 0 × 1 = 0, 1 × 0 = 0, 1 × 1 = 1, pouze výsledek je „1“, když je „1“;
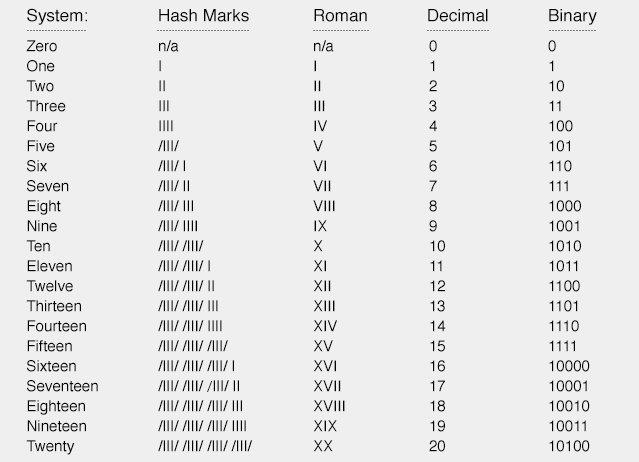
Kromě operace: Počet binárních čísel je pouze dvě čísla 0, 1, takže jeho obchodníci jsou 1 nebo 0.
logická operace
Aby bylo možné provádět různé zpracování binárních informací, je zapotřebí logická algebra. V logickém algexu existují tři nejzákladnější logické operace: logické plus (také známé jako operace "nebo" se symbolem "nebo", "nebo" + "), logika násobená (také známá jako, pomocí symbolu " And "," ∧ "nebo" · "indikováno) a inverzní (také známé jako "ne"operace, vyjádřeno jako symbol" nikoli "nebo" - "), což znamená, že:
logika plus: 0 ∨0 = 00 ∨1 = 11∨0 = 11∨1 = 1
logika vynásobená: 0 ∧ 0 = 00 ∧1 = 01 ∧0 = 01 ∧1 = 1
Logika není: "0" je "1", "1" je "0" po odrazu.
Diferenciální charakteristiky
1, pokud je hodnota binárního (celého) čísla 1, pak je toto číslo liché; pokud je tento bit 0, pak je toto číslo sudé.
2, je-li dolní N bit binárního čísla nula, lze toto číslo vydělit 2n.
3, pokud je binární číslo čísla jedna, zatímco ostatní jsou nula, pak je toto číslo rovno.
4, výsledek všech pozic bitového posunu doleva v binárním čísle se vynásobí dvěma.
5, výsledek jednoho bitu všech bezbitových binárních čísel je ekvivalentní číslu navíc ke dvěma (tato dvojice symbolů není použitelná).
6, obrácení všech bitů binárního čísla (to znamená, že se celá jedna změní na nulu, všechna nula se změní na jedničku) je ekvivalentní zpracování čísla (změna symbolu) mínus jedna.
7, maximální počet nesymbolických binárních čísel označených libovolným daným číslem je vždy nula.
8, výsledkem nulového dekrementování (redukovaného) je vždy maximální počet žádných symbolických binárních čísel reprezentovaných daným číslem.
