Въведение в проблема
18-ти век на Гобини, през него минава река, има два острова, има седем моста, свързващи два острова с брега на реката (като контурна карта). Някои хора предложиха въпрос: Как може пешеходецът да не повтаря, да не пропуска седемте моста наведнъж и накрая да се върне в началната точка. По-късно големият математик Еули го трансформира в геометрична задача - задача за рисуване. Той не само реши този проблем, но също така дава запълване на диаграма на картина: Броят на нечетните точки не е 0 е 2 (четният брой на нечетните числа, "ако е Четното число се нарича четно. Ако вие искате да нарисувате картина, трябва да имате равномерно нещо в средата, тоест има друг начин да имате друг начин и сингулярността може да е само в двата края, така че всяка фигура може да бъде нарисувана, Имахте ли или на двата края).
Метод на умозаключение
Когато Ойлер посети пруския Гобисбург (сега Русия Галонинград), той намери много интересна местна публика. Confuciate. В град Гобиник има река, наречена Прегел, това интересно забавление е разходка от всичките седем моста в събота, като всеки мост може да премине само веднъж и началната точка трябва да е едно и също място. .
Euchi поставя всяко парче в точка, свързваща два земни моста.
Невъзможно е да се пита по такъв начин. Неговият аргумент е следният, с изключение на началната точка, всеки път, когато човек влезе в земя (или точка) по мост, той (или тя) също ще напусне тази точка по друг мост. Следователно всяка линия е в точка, два моста (или линии) се изчисляват от линията от началната точка и линията на последната точка на връщане, така че броят на мостовете, свързани с друга земя, е почти четен.
Има проблем
Седем моста, няма точка, съдържаща броя на ориентациите, така че горните задачи не могат да бъдат изпълнени.
Ойлер е много важен, той също е много умен, той демонстрира уникалността на математика, който се занимава с практически проблеми - абстрахира действителен проблем в подходящ "математически модел". Този метод на изследване е „Метод на математическия модел“. Това не трябва да използва колко дълбока теория, но помислете за това, но за ключа за решаване на проблема.
След това Ойлер използва картина във фигурата, за да прецени насоките и бързо преценява, че 7-те моста не повтарят нито веднъж пристанището на Дойнсбург. С други думи, след колко години хората обръщат внимание на неповтарящия се маршрут, който изобщо не съществува. Проблем, който е бил труден за живеене, всъщност е толкова резервен отговор!
Крайно постижение
Първоначалният период на проблема
След като въпросът е повдигнат, много хора се интересуват много от това, но те експериментират, но От дълго време никога не съм бил решен. С обикновени математически познания, всеки мост се взема веднъж и седемте моста вървят общо 5040, и толкова много случаи, това ще бъде изпитание, което ще бъде много натоварване. Но как мога да намеря маршрут, който успешно минава през всеки мост, вместо да се повтаря? Поради това се формира известният „проблем на седемте моста Гособург“.
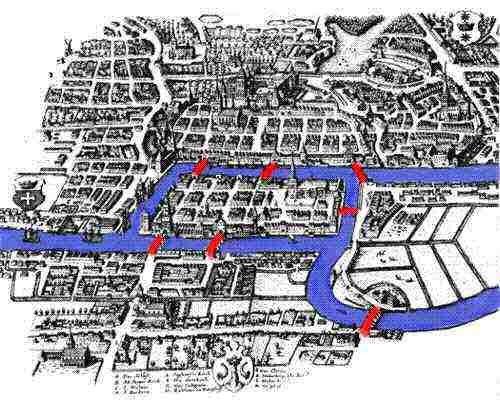
Проблем след експозиция
През 1735 г. няколко студенти пишат писмо до гениалния математик Еура, който работи в Русия, Порсопианската академия на науките. Помолете го да помогне за разрешаването на този проблем. Оу наблюдаваше Твърдия мост в Гоби, сериозно мислеше за него, но не успя да успее, така че подозираше, че въпросът Qiqiao не го решава?
През 1736 г., след едногодишно изследване, 29-годишният Орап представя документите за „Седем моста на Гоби“, успешно решава този проблем и създава нов клон на математиката – Теория на графиките.
В статията Eutu ще абстрахира проблема Qiqiao и ще вземе всяко парче в точка, свързваща два сухопътни моста. И по този начин получаваме същата геометрия, както е показано. Ако използваме A, B, C, D четири точки, за да представим четирите области на Гобиник. Такъв известен "проблем със седем моста" се преобразува в това дали е възможно да се използва неповтаряща се картина на седемте линии. Ако можете да рисувате, трябва да имате крайни точки и начални точки в графиката, а началната и крайната точка трябва да са еднакви. Тъй като симетрията може да се види от B или C като начална точка, ако се приеме, че A е началната точка и крайната точка, тогава трябва да има една далеч от жицата и съответната входна линия. Ако дефинираме броя на редовете на линията, влизаща в A, броят на редовете, които напускат жицата, е изход, а броят на прътите на линията е степен от A, тогава a Степента и степента на градусите са равни, тоест степента на А трябва да е четно число. Тоест, необходимо е да се направи десизор от А. Дегилността на дегилността трябва да е четно число, а степента на действително А е 5 е нечетна, така че може да се види, че е неподлежаща на подмяна от А. В същото време време, ако е от B или D, тъй като степените на B, D са 3, 3, всяка е нечетна, тоест началната точка е непубликувана.
Известно е, че горната причина е, че абстрактната математическа задача е несубалиптична, т.е. „седем мостови задачи” също не е публикувана.
From this we get: Euler loop relationship
Така че можем да знаем, че A графиката може да бъде начертана, трябва да отговаря на следните две условия:
1. Графиките трябва да са свързани.
2. Броят на "коефициентите" на фигурата е 0 или 2.
Можем също да проверим дали графиките могат да бъдат начертани. Може също така да се прецени да прецени "седемте мостови проблема", 4 точки са нечетни, може да знае, че картината не може да бъде "нарисувана", тоест няма многократно преминаване на всичките седем моста.
През 1736 г. Евкула обяснява своя метод за решаване в документите на „Гобинбургския мост 7“, които са предадени на Петербургската академия. Неговата индукция, поставяйки основите на новия математически клон - създаването на топологията.
Qiqiao Въпрос и теорема на Ойлер
Ойлер възприема изследването по въпроса Qiqiao, не само за да повтори проблема, предложен от жителите на Гобинбург, и получи и доказа три заключения, свързани с инсулт, и хората често се наричат теоремата на Ойлер. За свързваща карта обикновено се нарича Euler Road от маршрут, който е начертан от възел. Хората обикновено наричат чифт вериги на Ойлер, които са изтеглени обратно към началната точка. Картина с европейската верига се нарича карта на Ойлер.
Тази тема е включена в 12-та книга на Математика Математика. 104 страници.
Тази тема е включена и в първия том на първия том. На стр. 121.
Картина
⒈⒈⒈ ⒈ 通 通 通 图 图 图 图 图 图 图 图 图 图 图 通 图 图 图 图 图 图 图When you draw, you can take anything at the starting point, and finally you can draw this picture with this point.
⒉ Когато има само две нечетни перспективи (останалото е четно), трябва да се начертае. Когато рисувате, трябва да поставите странна точка като начална точка, а друга странна точка е край.
⒊ Други карти на състоянието не могат да чертаят. (Броят на нечетните точки може да се изчисли във втората фигура, за да се изтеглят няколко парчета.)
