Исторически фон
Повече от половин век преди раждането на Максуел хората са постигнали голям напредък в разбирането на електромагнитните явления. През 1785 г. френският физик К. А. Кулон (Charles A. Coulomb) установява закона на Кулон, описващ силата на взаимодействие между два точкови заряда въз основа на резултатите от експеримента за торсионен баланс. През 1820 г. H. C. Oersted (Hans Christian Oersted) открива, че електрическият ток може да отклонява магнитните стрелки, като по този начин свързва електричеството с магнетизма. След това А. М. Ампер (Andre Marie Ampère) изучава взаимодействието между електрическите токове и предлага много важни концепции и закона за веригата на Ампер. М. Фарадей (Майкъл Фарадей) има изключителен принос в много аспекти, особено закона за електромагнитната индукция, публикуван през 1831 г., който е важна теоретична основа за двигатели, трансформатори и друго оборудване.
През 1845 г. трите най-основни експериментални закона за електромагнитните явления: законът на Кулон (1785 г.), законът на Био-Савар (1820 г.), законът на Фарадей за електромагнитната индукция (1831 ~ 1845 г.) ) Бяха обобщени, концепциите на Фарадей за „силова линия " и "линия на магнитна сила" (сега наричана още "линия на електрическо поле" и "линия на магнитна сила") са развити в "концепцията за електромагнитно поле". От 1855 до 1865 г. Максуел прави цялостен преглед на закона на Кулон, закона на Био-Савар и закона на Фарадей и въвежда методите на математическия анализ в областта на електромагнитните изследвания, което води до раждането на електромагнитната теория на Максуел. .
Преди Максуел всички теории за електромагнитните явления се основаваха на концепцията за действие от разстояние. Смяташе се, че взаимодействието между заредени тела, намагнетизирани тела или проводници с ток може да се осъществи директно извън междинната среда. И това се прави незабавно, тоест скоростта на разпространение на електромагнитните смущения се счита за безкрайна. По това време само Фарадей имаше различни мнения. Той смята, че гореспоменатите взаимодействия са свързани с междинни медии и се осъществяват чрез прехвърляне на междинни медии, тоест застъпва теорията за индиректния трансфер.
Максуел наследява гледната точка на Фарадей, препраща към модела на механиката на течностите, прилага строги математически форми, за да обобщи работата на предшествениците си, предлага хипотезата за тока на изместване, разширява значението на тока и заключава основните закони на електромагнитното поле. четири диференциални уравнения, които са известните уравнения на Максуел. Той анализира този набор от уравнения, предвиждайки съществуването на електромагнитни вълни, и заключава, че скоростта на разпространение на електромагнитните вълни е крайна стойност (близка до скоростта на светлината) и че светлината също е електромагнитна вълна с определена честота. Той написа всичко по-горе в своята статия, озаглавена "За електричеството и магнетизма".
През 1887 г. Хайнрих Р. Херц използва експериментални методи за генериране и откриване на електромагнитни вълни, което потвърждава прозорливостта на Максуел. Между 1905 и 1915 г. теорията на относителността на Алберт Айнщайн допълнително демонстрира връзката между времето, пространството, масата, енергията и движението, показвайки, че електромагнитните полета са форма на материя и теорията за индиректността е призната.
Състав на уравнение
Уравненията на Максуел са съставени от четири уравнения:
Закон на Гаус: Този закон описва връзката между електрическото поле и разпределението на заряда в пространството. Линиите на електрическото поле започват с положителен заряд и завършват с отрицателен заряд (или безкрайност). Изчислете броя на линиите на електрическото поле, преминаващи през дадена затворена повърхност, тоест нейния електрически поток, и можете да знаете общия заряд, съдържащ се в тази затворена повърхност. По-подробно този закон описва връзката между електрическия поток, преминаващ през произволна затворена повърхност и заряда в затворената повърхност.
Магнитен закон на Гаус: Този закон показва, че магнитните монополи всъщност не съществуват. Следователно няма изолиран магнитен заряд и линията на магнитното поле няма начална точка и крайна точка. Линиите на магнитното поле ще се заобикалят или ще се простират до безкрайност. С други думи, линиите на магнитното поле, влизащи във всяка област, трябва да напуснат тази област. В терминологията магнитният поток, преминаващ през всяка затворена повърхност, е равен на нула или магнитното поле е пасивно поле.
Закон на Фарадей за индукция: Този закон описва как променящо се във времето магнитно поле индуцира електрическо поле. Електромагнитната индукция е теоретичната основа за производството на много генератори. Например, въртящ се прътов магнит генерира променливо във времето магнитно поле, което от своя страна генерира електрическо поле, карайки съседната затворена верига да индуцира ток.
Закон на Максуел-Ампер: Този закон гласи, че магнитното поле може да се генерира по два начина: единият е чрез провеждане на ток (оригиналния закон на Ампер), а другият е чрез променящо се във времето електрическо поле или ток на изместване (коригиращ член на Максуел) .
В електромагнетиката корекционният термин на Максуел означава, че променящо се във времето електрическо поле може да генерира магнитно поле, а поради закона за индукция на Фарадей, променящо се във времето магнитно поле може да генерира електрическо поле. По този начин двете уравнения теоретично позволяват на самоподдържащите се електромагнитни вълни да се разпространяват в пространството.
Основните точки на теорията за електромагнитното поле на Максуел могат да бъдат обобщени, както следва:
①Няколко отделни заредени обекта или тока, всички електрически и магнитни взаимодействия между тях се предават между тях Какво се предава в средната зона, независимо дали средната област е вакуум или физическо вещество.
②Електрическа енергия или магнитна енергия съществува не само в заредени тела, намагнетизирани тела или заредени обекти, но по-голямата част от нея се разпространява в околното електромагнитно поле.
③Ако има прекъсване във веригата, образувана от проводника, токът на проводимост във веригата ще бъде компенсиран от тока на изместване в диелектрика, т.е. пълният ток е непрекъснат. И връзката между тока на изместване и магнитното поле, което генерира, е същата като тази на тока на проводимост.
④ Магнитният поток няма нито начало, нито край, тоест няма магнитен заряд.
⑤Светлинните вълни също са електромагнитни вълни.
Има два начина за изразяване на уравненията на Максуел.
1. Интегралната форма на уравненията на Максуел е математически модел, който описва електромагнитното поле в определен обем или област. Изразът е:
Equation ① is the law of total current derived from the generalization of the law of Ampere’s loop, and its meaning is: the line integral of the magnetic field intensity H along any closed curve is equal to the area passing through the limited area of this curve Full current. The first term on the right side of the equal sign is the conduction current. The second term is the displacement current. Equation ② is the expression of Faraday's law of electromagnetic induction, which shows that the line integral of the electric field intensity E along any closed curve is equal to the negative value of the rate of change of the magnetic flux passing through the area defined by the curve with respect to time. The closed curve mentioned here does not necessarily have to be composed of conductors, it can be a dielectric loop, or even just any closed contour. Equation ③ represents the principle of magnetic flux continuity, indicating that for any closed curved surface, as much magnetic flux enters the curved surface, the same amount of magnetic flux leaves. That is to say, the B line has neither a beginning nor a terminal; it also shows that there is no magnetic charge corresponding to the electric charge. Equation ④ is the expression of Gauss's law, which shows that under time-varying conditions, the net flux of D from any closed surface should be equal to the sum of all free charges in the volume enclosed by the closed surface.
2. Уравнения на Максуел в диференциална форма. Диференциалната форма на уравненията на Максуел е за всяка точка в полето. Използвайки оператора del, те могат да бъдат записани като
Уравнение ⑤ е диференциалната форма на закона за общия ток, което показва, че кривата на интензитета на магнитното поле H е равна на общата плътност на тока в тази точка (плътност на тока на проводимост J и плътност на тока на изместване Сумата), т.е. източникът на вихровото магнитно поле е пълната плътност на тока, а токът на изместване може да генерира магнитното поле точно като тока на проводимост. Формула ⑥ е диференциалната форма на закона на Фарадей за електромагнитната индукция, която показва, че кривата на интензитета на електрическото поле E е равна на отрицателната стойност на скоростта на промяна във времето на плътността на магнитния поток B в тази точка, т.е. вихровият източник на електрическото поле е скоростта на промяна във времето на плътността на магнитния поток. Уравнение ⑦ е диференциалната форма на принципа на непрекъснатостта на магнитния поток, което показва, че дивергенцията на плътността на магнитния поток B винаги е равна на нула, т.е. линията B няма начало и край. Това означава, че няма магнитен заряд, съответстващ на електрическия заряд. Уравнение ⑧ е обобщение на закона на Гаус за електростатичното поле, тоест при променящи се във времето условия дивергенцията на електрическото изместване D все още е равна на плътността на свободния заряд в тази точка.
В допълнение към горните четири уравнения е необходима конститутивната връзка на средата
за да реши най-накрая проблема с решаването на количеството на полето. Където ε е диелектричната константа на средата, μ е пропускливостта на средата, а σ е проводимостта на средата.
Форма на изразяване
Интегрална форма
Интегралната форма на уравненията на Максуел е следната:
Това е 1873 г. Около годината Максуел предлага четири уравнения, изразяващи универсалния закон на електромагнитните полета. Между тях:
(1) описва природата на електрическото поле. Като цяло електрическото поле може да бъде електрическо поле със свободен заряд или индуцирано електрическо поле, възбудено от променящо се магнитно поле, а индуцираното електрическо поле е вихрово поле и неговата линия на електрическо изместване е затворена и не допринася за потока на затворена извита повърхност.
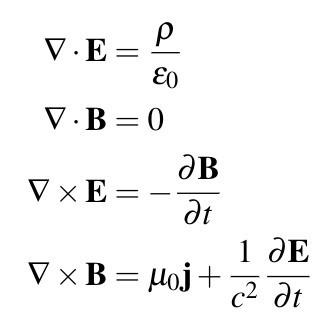
(2) описва природата на магнитното поле. Магнитното поле може да бъде възбудено от тока на проводимост или тока на изместване на променящото се електрическо поле. Всичките им магнитни полета са вихрови полета, а линиите на магнитната индукция са затворени линии, които не допринасят за потока на затворената извита повърхност.
(3) описва закона за променящото се магнитно поле за възбуждане на електрическото поле.
(4) описва закона за провеждане на ток и промяна на електрическото поле за възбуждане на магнитно поле.
Форма в стабилно поле
Кога
, уравненията се свеждат до уравненията на електростатичното поле и постоянното магнитно поле:
Форма в свободно пространство без източник на поле
Кога, the equation system becomes the following form:
The integral form of Maxwell's equations reflects the relationship between the amount of electromagnetic field (D, E, B, H) and the field source (charge q, current I) in a certain area of space.
Диференциална форма
При действителното приложение на електромагнитното поле често е необходимо да се знае връзката между количеството електромагнитно поле точка по точка в пространството и заряда и тока. От математическата форма интегралната форма на уравненията на Максуел се трансформира в диференциална форма. Обърнатият триъгълник е Хамилтониан.
Забележка:
(1) В различни инерциални отправни системи уравненията на Максуел имат еднакъв вид.
(2) За да се приложат уравненията на Максуел за решаване на практически проблеми, трябва да се вземе предвид и влиянието на средата върху електромагнитното поле. Например в еднаква и изотропна среда количеството електромагнитно поле има следната връзка с характеристиките на средата:
В нееднородна среда граничната стойност на количеството електромагнитно поле на интерфейса също трябва да се счита за връзка. Като се използва условието за начална стойност на величината на полето, когато t=0, по принцип може да се получи електромагнитното поле във всяка точка на пространството по всяко време, а именно E(x, y, z, t) и B(x, y, z, t).
По-долу са уравненията на Максуел в системата от единици на Гаус
Уравнения на физически свойства
Кога there is a medium, due to electric and magnetic fields The interaction with the medium makes the amount of electromagnetic field related to the characteristics of the medium. Therefore, the above-mentioned Maxwell equations are not complete at this time, and the physical property equations describing the properties of the medium (isotropic medium) need to be supplemented, respectively
Във формулата ε, μ и σ са абсолютната диелектрична константа, абсолютната пропускливост и проводимост на проводника, съответно Rate.
Допълнително теоретично доказателство, че уравненията на Максуел и уравненията на физическите свойства заедно са пълен набор от уравнения за определяне на промените на електромагнитното поле. Тоест, когато зарядът и токът са дадени, промяната на електромагнитното поле може да бъде напълно определена от горното уравнение според началните условия (и необходимите гранични условия). Разбира се, ако искате да обсъдите ефекта на електромагнитното поле върху заредените частици и движението на заредените частици в електромагнитното поле, имате нужда и от формулата за силата на Лоренц.
Сложна числова форма
За синусоидални променливи във времето полета комплексните вектори могат да се използват за изразяване на закона на електромагнитните полета като комплексни числа.
В закона за комплексното електромагнитно поле, тъй като комплексната величина на полето и величината на източника са само функции на позицията в пространството, когато се решава, не е необходимо да се разглежда тяхната зависимост от времето. Следователно е по-удобно да се използва сложният закон на електромагнитното поле, за да се обсъди синусоидалното променливо във времето поле.
Забележки
Използвайки различни системи от единици, формата на уравненията на Максуел ще бъде леко променена и общата форма ще остане същата, но различни константи ще се появят на различни позиции в рамките на уравнението.
Международната система от единици е най-често използваната система от единици. Цялата инженерна област използва тази система от единици. Повечето химици също използват тази система от единици. Почти всички учебници по физика в колежа използват тази система от единици. Система. Други често използвани единици са единиците Гаус, Лоренц-Хевисайд и Планк. Единичната система на Гаус, получена от системата сантиметър-грам-секунда, е по-подходяща за учебни цели и може да направи уравненията да изглеждат по-прости и по-лесни за разбиране. Единичната система на Лоренц-Хевисайд също произлиза от системата сантиметър-грам-секунда и се използва главно във физиката на елементарните частици; Единичната система на Планк е естествена единична система и нейните единици се определят според естеството на природата. Зададен от мъж. Единичната система на Планк е много полезен инструмент за изучаване на теоретична физика и може да даде голямо просветление. На тази страница, освен ако не е посочено друго, всички уравнения са в Международната система единици.
Тук са показани два еквивалентни израза на уравненията на Максуел. Първият израз е както следва:
Този израз добавя свободния заряд и свързания заряд към общия заряд, изискван от закона на Гаус, и също така разделя свободния ток, свързания ток и поляризационния ток. Общият ток е общият ток в закона на Максуел-Ампер. Този израз приема сравнително основна и микро гледна точка. Този израз може да се приложи за изчисляване на електрическите и магнитните полета, генерирани от ограничен източник на заряд и източник на ток във вакуум. В действителност обаче има твърде много електрони и атомни ядра в материята, които не могат да бъдат включени в изчислението. Всъщност класическият електромагнетизъм не се нуждае от толкова точни отговори.
За втория израз, моля, вижте „общия формуляр“ в гореспоменатия „формуляр за интегриране“. Той приема свободен заряд и свободен ток като източник и не изчислява директно приноса на свързания заряд, появяващ се в диелектрика, и свързания ток и поляризационния ток, появяващ се в магнетизираното вещество. Тъй като в общи действителни условия параметрите, които могат да бъдат пряко контролирани, са свободен заряд и свободен ток, а свързаният заряд, свързаният ток и поляризационният ток са явления, които възникват, след като веществото е поляризирано. Използването на този израз ще направи диелектрика или намагнитването. Различните физически изчисления в рамките на веществото са по-лесни.
На пръв поглед уравненията на Максуел изглеждат свръхдетерминирани. То има само шест неизвестни (векторното електрическо поле и магнитното поле имат по три неизвестни, токът и зарядът не са неизвестни. Това е физическа величина, която се задава свободно и съответства на запазването на заряда), но има осем уравнения (две гаусови законите имат две уравнения, законът на Фарадей и законът на Ампер са векторни, всяко от които съдържа три уравнения). Тази ситуация е свързана с ограничената повторяемост на уравненията на Максуел. От теорията може да се заключи, че всяка система, която удовлетворява закона на Фарадей и закона на Ампер, трябва да отговаря на два закона на Гаус.
От друга страна, уравненията на Максуел не са затворени. Само предвид характеристиките на електромагнитната среда тази система от уравнения може да получи определено решение.
Приложима скала
The Maxwell equations are usually applied to the "macro average field" of various fields. Кога the scale shrinks to the microscopic scale, so as to approach the size of a single atom, the local fluctuations of these fields will become unignorable, and quantum phenomena will begin to appear. Only under the premise of macro-average, some physical quantities such as the permittivity and permeability of a substance can get meaningful definition values.
Радиусът на най-тежкото ядро е около 7 фемтометъра (1fm=10-15m). Следователно в класическата електромагнетика микроскопичният мащаб се отнася до порядъка на величина, по-голям от 10-14m. За да отговарят на микроскопичния мащаб, електроните и ядрата могат да се разглеждат като точкови заряди и се установяват микроскопичните уравнения на Максуел; в противен случай трябва да се вземе предвид разпределението на заряда вътре в ядрото. Електрическото поле и магнитното поле, изчислени в микроскопичен мащаб, все още се променят доста драстично, разстоянието на пространствена промяна е по-малко от 10-10m, а периодът на промяна във времето е между 10-17 и 10-13 секунди. Следователно, от микроскопичните уравнения на Максуел трябва да се извърши класическата операция за осредняване, за да се получи гладко, непрекъснато и бавно променящо се макроскопично електрическо поле и макроскопично магнитно поле. Най-ниската граница на макро скалата е 10-8 метра. Това означава, че поведението на отражение и пречупване на електромагнитните вълни може да се опише с макро-уравненията на Максуел. Приемайки тази минимална граница като дължина на страната, куб с обем от 10-24 кубически метра съдържа приблизително 106 ядра и електрони. Физическото поведение на толкова много ядра и електрони, след класическо осредняване, е достатъчно, за да изглади всякакви бурни флуктуации. Според надеждни литературни записи, класическата операция за осредняване изисква само осредняване в пространството, не във времето, и не е необходимо да се вземат предвид квантовите ефекти на атомите.
Значение
Приносът на Максуел за създаването на концепцията за полето също е голяма иновация във физиката по онова време, защото именно появата на концепцията за полето направи много физици Учените успяха да се отърват от оковите на "концепцията за супер-разстояние" на Нютон и общоприетата идея, че електромагнитните и гравитационните ефекти са "близост".
Позицията на уравненията на Максуел в електромагнетиката и класическата електродинамика е същата като позицията на законите за движение на Нютон в Нютоновата механика. Електромагнитната теория, базирана на уравненията на Максуел, е едно от най-гордите постижения на класическата физика. Съвършеното единство на електромагнитното взаимодействие, разкрито от него, е установило убеждението на физиците, че различните взаимодействия на материята трябва да бъдат обединени на по-високо ниво. Тази теория се прилага широко в техническите области.
Научна значимост
(1) Класическата теория на полето е основана от Максуел в края на 19-ти век въз основа на обобщаване на трите експериментални закона на електромагнетизма и сравняването им с механични модели. Но основното постижение на Максуел му позволява точно да излезе от ограниченията на рамката на класическата механика: във физиката той приема „полето“ вместо „силата“ като основен изследователски обект и въвежда векторна частична диференциална операция, която е различна от класическа математика в математиката. Символ. Тези две са в основата на откриването на уравнението на електромагнитната вълна. С други думи, работата на Максуел всъщност е пробила рамката на класическата физика и математика по онова време, но поради историческите условия по това време, хората все още могат да разберат теорията за електромагнитното поле само от рамката на смятането на Нютон и класическата механика .
Съвременната математика, математическият анализ в Хилбертовото пространство се появява едва в началото на 19 век и 20 век. Концепцията за вълните на материята в квантовата механика е открита по-късно, особено неразривната математическа логическа връзка между съвременната математика и квантовата физика все още не е напълно разбрана и приета от хората. От установяването на теорията на електромагнитното поле от Максуел до сега хората винаги са използвали класическата математика в Евклидовото пространство като основен метод за решаване на уравненията на Максуел.
(2) От появата, формата, съдържанието и историческия процес на уравненията на Максуел можем да видим: Първо, физическият обект се развива в нов израз на аксиома на по-дълбоко ниво. След като бъде овладян от човечеството, научният прогрес няма да се развива според установени предпоставки. Създаването на нова аксиомна система с когнитивно значение е знак за научно-теоретичен прогрес. Второ, въпреки че физическият обект и начинът на изразяването му са различни неща, невъзможно е да се признае „съществуването“ на този обект, без да се разчита на подходящ метод на изразяване. Трето, теорията, която изграждаме, ще определи нивото на значение, в което превръщаме нашите обекти във физически факти. Точно това е объркването, което ни донесе съвременната авангардна физика.
(3) Уравненията на Максуел разкриват красотата на симетрията във взаимната трансформация на електрически и магнитни полета. Тази красота е напълно изразена в съвременна математическа форма. Въпреки това, от една страна, трябва да признаем, че само правилната математическа форма може напълно да демонстрира целостта (електромагнитна симетрия), която не може да се види в емпиричния метод; от друга страна, не трябва да забравяме, че красотата на тази симетрия е в математическа форма. Единната природа на отразеното електромагнитно поле. Следователно трябва да осъзнаем, че трябва да „открием“ или „видим“ тази симетрия в математическите изрази, вместо директно да изведем тази същност от физическите математически формули.
