Ко-различна матрица

концепция

при условие, че

е n-измерна случайна променлива, споменатата матрица

n-мерна случайна променлива

ковариационна матрица (ковариационна матрица), наричана също

, където

към

компонент

и

ковариация (при условие, че са налице).

Например двумерна случайна променлива

на ковариационната матрица

където <раздел>

Тъй като

, ковариационната матрица е неотрицателна определена симетрична матрица.

свойства

ковариационна матрица със следните свойства:

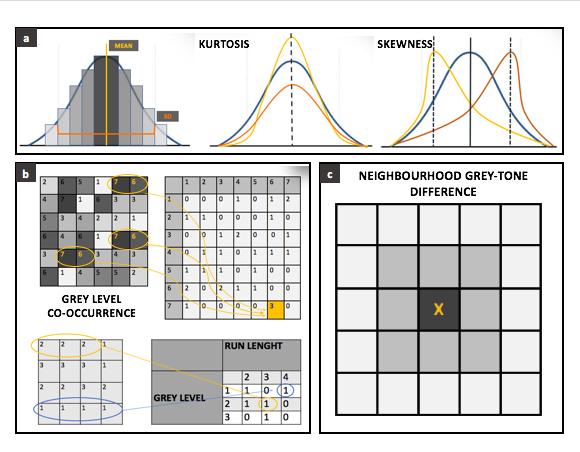
(1) <раздел>

(2).

, където A е матрица, b е вектор.

(3) <раздел> .

Приложения

ковариационната матрица може да се използва за представяне на многомерни случайни променливи с плътност на вероятността, като по този начин изследването на многомерни случайни променливи може да бъде постигнато чрез ковариационната матрица. Двуизмерна случайна променлива

като пример, тъй като

вградена матрица

<раздел> , <раздел>

и

ковариационна матрица

така наличен

Оттогава

Така

от плътността на вероятността

това уравнение може да се обобщи до n-мерно нормално разпределение.