дефиниция
хипотеза функция и в област в Анализ, има обща част с , която трябва да бъде установена, така че и Вижте числовата колекция на всички точки в и , в < В / Раздел> Анализ, в <раздел> , в <раздел> .
функция Можете да видите дефинираната област на разширение , която се нарича резолюция на . Разбира се, според същата причина, е синтактичен анализ, този начин за разширяване на оригинала, за да функционира, наричан разширител на синтактичен анализ .
иска да придаде значение на този метод, трябва да даде само единствения резултат при подходящите условия, ние ще докажем, че е вярно, преди да го дадем, първо споменаване, ако Подобен метод е дефиниран за единицата реална функция , какво трудно ще се срещне.
е зададено в , , хората естествено ще препоръчат използването на тази формула за разширяване на дефиницията на към други < / раздел>. Трудностите обаче са, че две различни формули могат да имат една и съща функция в определен диапазон, но в друг интервал, различни функции и няма очевидна причина да се определи коя формула е „просто“. Например в горната функция може да се използва и като величина
е равно на .
Това ниво е непоследователна конвергенция, но дори ако едно и също нещо се сближи единодушно, същото нещо ще се случи, като например броя на нивата
<раздел> в един включен < Секция>интервал единодушно се сближава; ако го използва, не е надеждата, че числото на числото на и от положителния не се надява, Exvelor of Section> е .
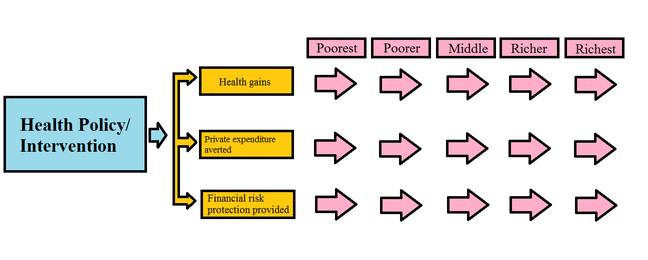
Тъй като общата дефиниция на функция за анализ
функцията за анализ често се дефинира в определена ограничена област на равнината, принципите на разширяване ни карат да дефинираме дефиниция, която има Всяка функция за анализ на всяка специална област , което се състои от цялото разширение на оригиналната функция и оригиналната функция и всички тези разширения. По този начин можем да дефинираме функции във всички или да ги дефинираме във всяка точка извън някои специални точки, или само определена граница в равнината. Има определение в района, но вече не го преодолявате. В крайната ситуация регионът е зоната на съществуване на функцията и нейната граница се нарича естествена граница на функцията. За случая на функции с много стойности ще получим множество различни стойности на функцията за някои z или за всички Z. .
Изглежда, че тази дефиниция зависи от специалната дефиниция на функциите, които стартирахме, но връзката между двете взаимно разширения е обратима, така че всички процеси могат да бъдат обърнати. Елате, така че това определение всъщност не е свързано с някаква специална отправна точка.
Стандартният метод на Dandu
стандартният метод за разширяване е методът на нивото на мощността, ако приемем, че започваме от броя на оценките
Той се събира в кръгова . Вземете точка B в кръга, изчислете стойността на и стойността на разделителите Mode. Това ниво трябва да се събира във всеки кръг от B като център и напълно да попада в оригиналния кръг, който също може да се събира в по-голям кръг, осигурявайки функция за разделителна способност на функцията, така че цялата функция може да се конфигурира чрез нивото на мощност. Всяко ниво на мощност или всеки набор от стойности <раздел> <раздел> <раздел> <раздел> <раздел> от него се нарича функция.
Следващата теорема илюстрира причината, поради която стойността, получена от който и да е метод за разширение, може да бъде получена и чрез метод за мощност.
Вие C е точка на свързване z = a и Z = b, по тази обиколка използвахме някакъв начин за разширяване на , Има формула, която дефинира в областта и има естеството на вторичния: (i) всяка точка от C е една или множество D n от вътрешната точка ; (ii) последователните се припокриват един с друг и в публичната част различните дефиниции на имат една и съща стойност.
Трябва да използваме метода на ниво на мощност, за да постигнем това, т.е. да намерим списък , за да накараме събиращата се окръжност във всяка точка в колоната да съдържа следващата точка и Стойността, получена от методът на степенните редове е същият като другия метод. По този начин то ще може да достигне B след ограничени множество стъпки.
За всяка точка от C има положителен радиус на конвергенция е непрекъсната функция на Z, ако За съседните две точки и радиуса на сближаване на таблицата "Section> и ", section> . Тъй като е в кръга на радиуса в като радиус, той се извлича от теоремата на Cori Pleulele за
, използвайте същия метод, но използвайте
< Раздел><раздел> Тъй като е <раздел> , във всеки случай е <раздел> (2) постоянен. Заедно (1) и (2) е доказано, че когато е , това е резултат от нуждата.
Тъй като е непрекъснат, той ще може да получи долната стойност по подразбиране; тъй като е константа, трябва да е положително число, задайте това уверение на .
Започваме от , ред е точка по протежение на разстоянието и Разстояние, равно на , то В рамките на кръга на сближаване в точка, функцията показва функцията, показваща степенния ред на , новият радиус на конвергенция е най-малко , така че може да достигне кривата и точка A от < section> , последвано от този метод, е ясно, че ще стигне до B след ограничено време. Що се отнася до стойността на B, получена чрез този метод, фактът, че е равен на други методи, може да бъде стартиран от обща уникалност.

